☠WEEDINATOR☠ חלק 4: קוד גיאומטריה של היגוי דיפרנציאלי: 3 שלבים

2024 מְחַבֵּר: John Day | [email protected]. שונה לאחרונה: 2024-01-30 09:17

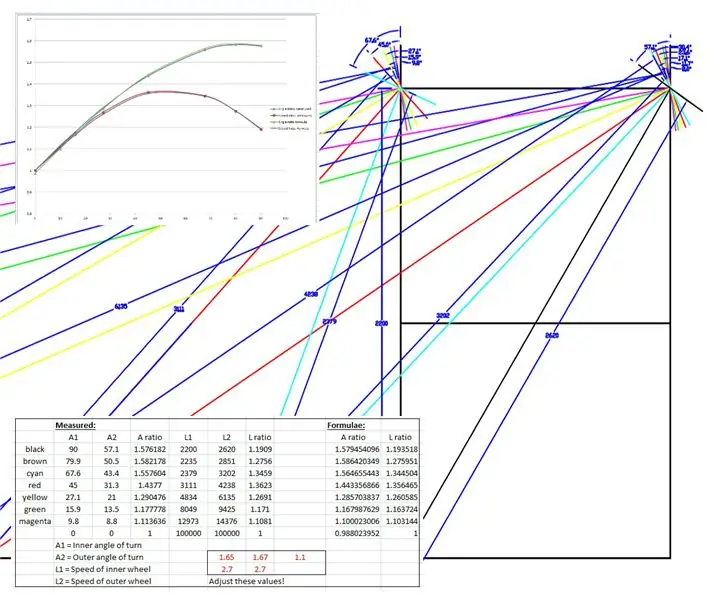
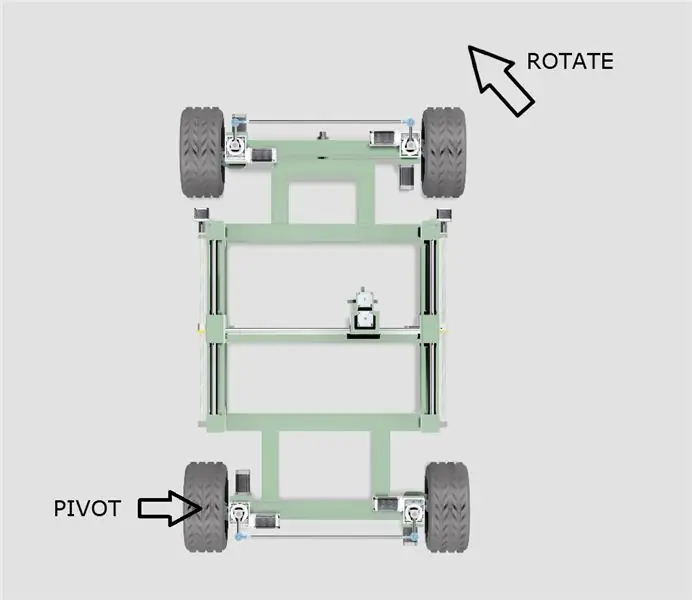
אם יש לך זמן לצפות בסרטון הנ ל, תבחין שיש כמה רעשים מוזרים שנגרמים על ידי המנועים על ההיגוי שנעצרים מדי פעם כשה WEEDINATOR מנווט סיבוב של 3 נקודות. המנועים בעצם נתקעים זה בזה מכיוון שרדיוס הסיבוב שונה מבפנים כלפי חוץ והמרחק שהגלגל עובר שונה לפי דרגת סיבוב.

ניתן לחשב את הגיאומטריה של הסיבוב על ידי שרטוט של 8 תמורות בערך של הסיבוב, תוך מתן דוגמאות לסיבוב בזוויות שונות בגלגל הפנימי מ -0 (ללא סיבוב) ל -90 (נעילה מלאה). נשמע מסובך?

רוב הרובוטים הקטנים עם הגלגלים אינם מנסים לקבל כל סוג של היגוי מתוחכם והם מסתמכים, ביעילות רבה, על שינוי המהירות היחסית של המנועים מכל צד של הרכב, וזהה בערך לאופן שבו חופר או טנק עוקבים. עובד. זה נהדר אם אתה טוען מעל אזור מלחמה מלא במכתש ויורה על כל מה שזז, אבל בסביבה חקלאית שלווה חשוב לפגוע כמה שפחות באדמה ובקרקע, כך שחריקת גלגלים קדימה ואחורה אחד נגד השני היא לא ראוי!

לרוב המכוניות והטרקטורים יש גאדג'ט שימושי מאוד שנקרא 'דיפרנציאל', למעט המכוניות שאתה רואה בסרטים אמריקאים ישנים שבהם אתה יכול לשמוע את הצמיגים צורחים כמו מטורפים בכל פעם שהם עוברים פינה. האם האמריקאים עדיין בונים מכוניות כאלה? עם WEEDINATOR, אנו יכולים לתכנת דיפרנציאל למנועי ההנעה על ידי חישוב הנוסחה למהירויות ולזוויות היחסיות של הגלגלים בכל זווית סיבוב מסוימת. עדיין נשמע מסובך?

להלן דוגמא מהירה:

אם ה- WEEDINATOR מנווט סיבוב ויש לו את הגלגל הפנימי שלו ב 45 מעלות, הגלגל החיצוני הוא לא 45 מעלות, זה יותר כמו 30 מעלות. כמו כן, הגלגל הפנימי עשוי להסתובב במהירות של 1 קמ"ש, אך הגלגל החיצוני יהיה מהיר יותר באופן משמעותי, יותר כמו 1.35 קמ"ש.

שלב 1: הגדרת גיאומטריה

יש להניח כמה הנחות יסוד מלכתחילה:

• השלדה מסתובבת באחד הגלגלים האחוריים כפי שמוצג בתרשים למעלה.
• המרכז האפקטיבי של מעגל הציר ינוע לאורך קו המורחב ממרכזי שני הגלגלים האחוריים, בהתאם לזווית הסיבוב.
• הגיאומטריה תהיה בצורת עקומת סינוס.

שלב 2: ציורים מוקטנים של זוויות גלגלים ורדיוסים

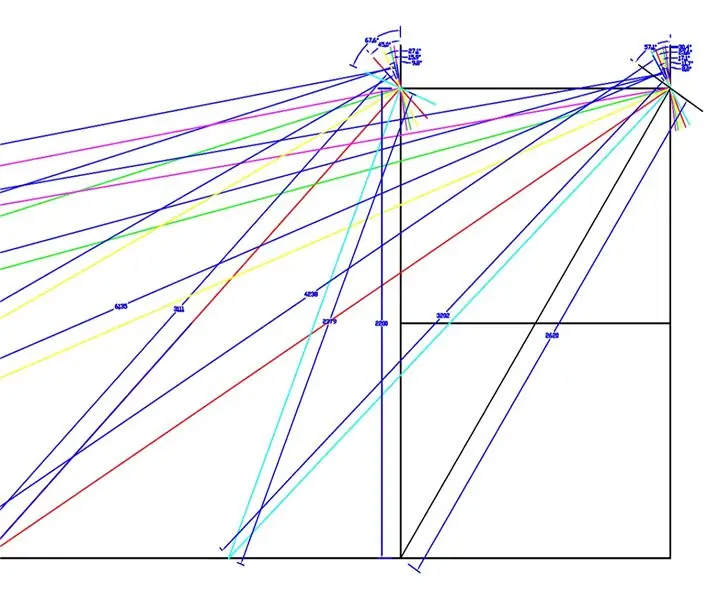
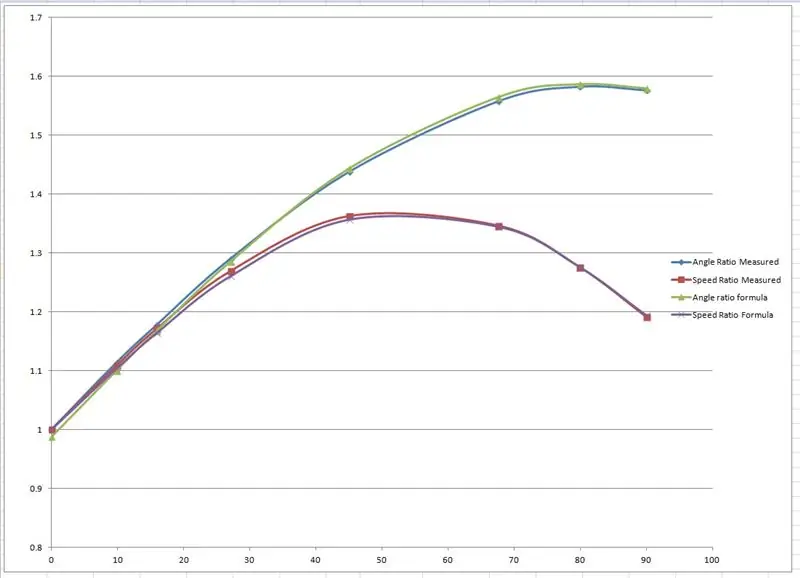
ציור בקנה מידה מלא נעשה על הגלגלים הקדמיים והשלדה של WEEDINATOR עם 8 תמורות שונות של זווית גלגל פנימית בין 0 ל -90 מעלות ומרכזי הפנייה בהתאמה מפותים כפי שמוצג בשרטוטים למעלה.

הרדיוסים האפקטיביים נמדדו מהציור ושרטטו על גרף ב- Microsoft Excel.

הופקו שני גרפים, אחד מהיחס בין ציר הגלגל הקדמי השמאלי והימני והשני ליחס בין שתי הרדיוסים לכל זווית סיבוב מסוימת.

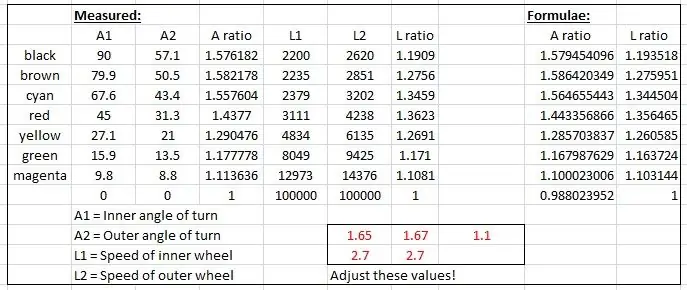
לאחר מכן ניסיתי לנסח כמה נוסחאות כדי לחקות את התוצאות האמפיריות המבוססות על עקומת סינוס. אחד הפאדג'ים נראה כך:

speedRatio = (חטא (פנימי*1.65*pi/180) +2.7) /2.7; // פנימי הוא זווית הפנייה הפנימית.

הקימורים התעלפו על ידי שינוי הערכים המוצגים באדום בקובץ האקסל עד שהקימורים השתלבו.

שלב 3: קידוד הנוסחאות

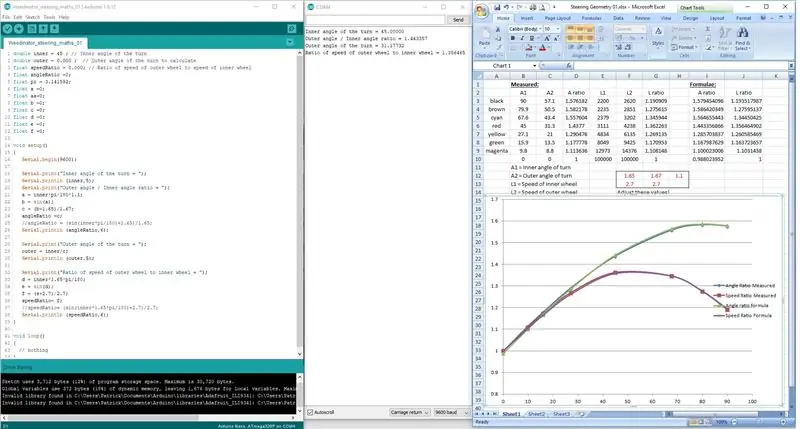
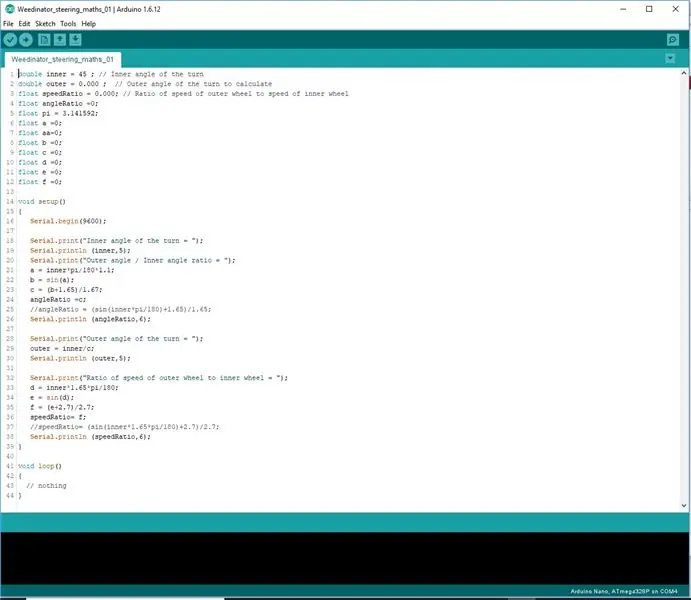
במקום לנסות לקודד את הנוסחאות בשורה אחת, הן חולקו לשלושה שלבים כדי לאפשר לארדואינו לעבד את המתמטיקה כראוי.

התוצאות מוצגות בתצוגת היציאה הסדרתית ונבדקות עם התוצאות הנמדדות בשרטוט הסקאלה.