
תוכן עניינים:
- מְחַבֵּר John Day day@howwhatproduce.com.
- Public 2024-01-30 09:12.
- שונה לאחרונה 2025-01-23 14:46.


מדידת תדירות מהאות שנתפס יכולה להיות משימה קשה, במיוחד בארדואינו מכיוון שיש לה כוח חישוב נמוך יותר. ישנן שיטות זמינות ללכידת מעבר אפס שבו התדירות נלכדת על ידי בדיקה כמה פעמים האות חוצה קווים אפס בתוך הזמן הנתון. שיטה כזו עשויה שלא לפעול כאשר האות הוא שילוב של תדרים שונים.
איכשהו קשה לקודד את זה אם אתה לא מרקע כזה. אבל בהיותו מתעסק הקוד הזה עשוי להיות שימושי מאוד לפרויקטים שונים הקשורים למוזיקה, ניתוח אותות. המניע של הפרויקט הזה היה להכין קוד שקל ליישום על Arduino מבלי להיכנס לרקע שלו.
פרויקט זה אינו מסביר את העבודה של FFT אך מסביר את היישום של הפונקציה FFT. אותו תהליך מוסבר גם בסרטון המצורף.
אם אתה מעוניין רק ביישום הקוד ולא בהסבר שלו. אתה יכול לדלג ישירות לשלב מס '3.
שלב 1: מבוא לשינוי תדרים


כל אות יכול להיות מורכב משילוב של גלי סינוסואידיים שונים. כך שניתן להציג גם כל אות מבוסס זמן כשילוב של הסינוס השונות של אמפליטודות שונות.
ניסיתי להסביר את פעולתו של DFT (טרנספורמציה פורטית דיסקרטית) באחד מההנחיות הקודמות (https://www.instructables.com/id/Arduino-Frequency…). שיטות אלה איטיות במיוחד עבור כל יישום בזמן אמת. מה שהופך אותו כמעט חסר תועלת.
בתמונה מוצג אות שהוא שילוב של שני תדרים f2 ו- f5. אות זה מוכפל בגלי סינוס הבדיקה של ערכים f1 עד f5.
ניתן להראות מתמטית שסיכום של ריבוי של שתי מערכי נתונים הרמוניים בעלי תדירות שונה נוטה לאפס (מספר נתונים גבוה יותר יכול להוביל לתוצאה של בלילה). במקרה שלנו, אם לשני תדרי הכפל הללו יש תדר זהה (או קרוב מאוד), סכום ההכפלה הוא המספר האפס.
אז אם האות שלנו יוכפל בסיכום f1 הכפל יהיה אפס (קרוב לאפס ליישום אמיתי). דומה במקרה של f3, f4. אולם מבחינת הערך, פלט f2 ו- f5 לא יהיה אפס, אך גבוה משמעותית משאר הערכים.
כאן האות נבדק עם 5 תדרים, ולכן צריך להכפיל את האות בחמישה תדרים. חישוב כה אינטנסיבי לוקח זמן גבוה יותר. מבחינה מתמטית מוצג כי עבור N מספר דגימות הוא דורש כפל N*N מורכב.
שלב 2: טרנספורמציה מהירה של פורייה
כדי להפוך את החישוב של DFT למהיר יותר, אלגוריתם FFT פותח על ידי ג'יימס קולי וג'ון טוקי. אלגוריתם זה נחשב גם לאחד האלגוריתמים החשובים של המאה ה -20. הוא מחלק אות לחלק מוזר ואפילו ברצף, מה שמוריד מספר חישובים נדרשים. על ידי שימוש בו ניתן לצמצם את הכפל המורכב הנדרש ל- NlogN. שזה שיפור משמעותי.
תוכל להתייחס להלן הפניות שאליהן התייחסתי בעת כתיבת הקוד להבנה מפורטת של המתמטיקה שמאחורי FFT:
1.
2.
3.
4.
שלב 3: הסבר על הקוד
1. סינוס מהיר וקוסינוס:
חישוב FFT לוקח את הערך של סינוס וקוסינוס שונים מספר פעמים. הפונקציה המובנית של Arduino אינה מהירה מספיק ולוקחת זמן רב כדי לספק את הערך הנדרש. מה שהופך את קוד איטי באופן משמעותי (מכפיל את הזמן ל -64 דוגמאות). כדי להתמודד עם נושא זה ערך סינוס עבור 0 עד 90 מעלות מאוחסן ככפולה של 255. פעולה זו תבטל את הצורך בשימוש במספרים כצף ונוכל לאחסן אותו כבייט שלוקח 1/4 מקום על Arduino. Sine_data צריך להדביק בראש הקוד כדי להכריז עליו כמשתנה גלובלי.
מלבד sine_data, מערך בשם f_peaks הכריז כמשתנה גלובלי. לאחר כל הפעלה של פונקציית FFT מערך זה מתעדכן. כאשר f_peaks [0] הוא התדר הדומיננטי ביותר וערכים נוספים בסדר יורד.
בת sinus_data [91] = {0, 4, 9, 13, 18, 22, 27, 31, 35, 40, 44, 49, 53, 57, 62, 66, 70, 75, 79, 83, 87, 91, 96, 100, 104, 108, 112, 116, 120, 124, 127, 131, 135, 139, 143, 146, 150, 153, 157, 160, 164, 167, 171, 174, 177, 180, 183, 186, 189, 192, 195, 198, 201, 204, 206, 209, 211, 214, 216, 219, 221, 223, 225, 227, 229, 231, 233, 235, 236, 238, 240, 241, 243, 244, 245, 246, 247, 248, 249, 250, 251, 252, 253, 253, 254, 254, 254, 255, 255, 255, 255}; float f_peaks [5];
מכיוון שאחסנו ערך סינוס עבור 0 עד 90 מעלות ניתן לחשב כל ערך של סינוס או קוסינוס. מתחת מתפקדים הסיבוב הראשון של המספר לנקודה עשרונית אפסית וערך החזרה מהנתונים המאוחסנים. לשיטה זו צריך רק חלוקה צפה אחת. ניתן לצמצם זאת עוד יותר על ידי אחסון ישיר של ערכי סינוס (לא 255 מרובים). אבל זה אוכל זיכרון גבוה בארדואינו.
שימוש בהליך הנ ל מפחית את הדיוק אך משפר את המהירות. עבור 64 נקודות, זה נותן את היתרון של 8ms ו עבור 128 נקודות זה נותן את היתרון של 20ms.
שלב 4: הסבר על קוד: פונקציית FFT
ניתן לבצע FFT רק בגודל המדגם 2, 4, 8, 16, 32, 64 וכן הלאה. אם הערך אינו 2^n, הוא יקח את הצד התחתון של הערך. לדוגמה, אם נבחר את גודל המדגם של 70 אז הוא ישקול רק את 64 הדגימות הראשונות ותשמיט מנוחה.
תמיד מומלץ שיהיה גודל מדגם של 2^n. שיכול להיות:
2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, …
שתי מצפות out_r ו- out_im ידרשו כמות גבוהה של זיכרון. עבור Arduino nano לא יעבוד עבור דוגמאות גבוהות מ- 128 (ובמקרים מסוימים 128) בגלל חוסר זיכרון זמין.
נתוני int לא חתומים [13] = {1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048};
int a, c1, f, o, x; a = N; עבור (int i = 0; i <12; i ++) // חישוב הרמות {if (data <= a) {o = i;}} int in_ps [data [o] = {}; // קלט לרצף float out_r [data [o] = {}; // חלק אמיתי של transform float out_im [data [o] = {}; // חלק דמיוני של טרנספורמציה
זרימה נוספת היא כדלקמן:
1. הקוד יוצר קצת הפוך את הסדר לגודל המדגם הנתון (פרטים על היפוך סיביות בהפניות: שלב 2)
2. נתוני קלט שהוזמנו לפי הזמנה שנוצרה, 3. בוצע FFT
4. משרעת המספר המורכב המחושב, 5. פסגות מזוהות ומוזמנות בסדר יורד
6. ניתן לגשת לתוצאות מתוך f_peaks.
[כדי לגשת לנתונים אחרים (מלבד תדר שיא) יש לשנות את הקוד, כך שניתן להעתיק משתנה מקומי למשתנה גלובלי מוגדר מראש]
שלב 5: בדיקת הקוד


גל משולש לדוגמא ניתן כקלט. עבור תדירות דגימת גל זו היא 10 הרץ ותדירות הגל עצמה היא 1.25 הרץ.
כפי שניתן להראות מהתפוקה הגולמית, הערך תואם את ה- FFT המחושב על ידי Scilab. עם זאת, ערכים אלה אינם זהים בדיוק לאותנו דיוק נמוך אך גל סינוס מהיר יותר.
בתדר המוצא תדר מערך הם 1.25 ו 3.75. אין צורך לקבל את הערך המדויק בכל פעם. בדרך כלל מספרים אלה נקראים פחי תדרים. כך שער הפלט עשוי להיות בכל מקום בתוך הפחים שצוינו.
מְהִירוּת:
עבור Arduino nano זה לוקח:
16 נקודות: 4ms32 נקודות: 10ms 64 נקודות: 26ms 128 נקודות: 53ms
שלב 6: מסקנה
ניתן להשתמש בקוד FFT זה ביישומים בזמן אמת. מכיוון שלוקח בערך 30 אלפיות השנייה להשלים את החישוב. עם זאת, הרזולוציה שלה מוגבלת במספר דוגמאות. מספר המדגם מוגבל על ידי זיכרון Arduino. באמצעות Arduino Mega או דיוק לוח ביצועים גבוה יותר אחר ניתן לשפר.
אם יש לך שאלות, הצעות או תיקונים, אל תהסס להגיב.
עדכון (2/5/21)
עדכונים: // ----------------------------- פונקציית FFT --------------- ------------------------------- // float FFT (int in , int N, Frequency float)
סוג הנתונים של N השתנה למספר שלם (בייט קיים) לתמיכה> 255 גודל מדגם. אם גודל המדגם הוא <= 128, יש להשתמש בסוג נתוני בתים.
מוּמלָץ:
חיישן טמפרטורה עבור Arduino מיושם עבור COVID 19: 12 שלבים (עם תמונות)

חיישן טמפרטורה עבור Arduino מיושם עבור COVID 19: חיישן הטמפרטורה עבור Arduino הוא מרכיב בסיסי כאשר אנו רוצים למדוד את הטמפרטורה של מעבד של גוף האדם. חיישן הטמפרטורה עם Arduino חייב להיות במגע או קרוב כדי לקבל ולמדוד את רמת החום. כך לא
QuickFFT: FFT במהירות גבוהה עבור Arduino: 3 שלבים

QuickFFT: FFT במהירות גבוהה עבור Arduino: ל- Arduino אופייני יש זיכרון RAM מוגבל וכוח עיבוד, ו- FFT הוא תהליך אינטנסיבי לחישוב. עבור יישומים רבים בזמן אמת, הדרישה היחידה היא לקבל תדר עם משרעת מרבית או נדרש לזהות שיאי תדרים. באחד מ
ביטול הארגז של ג'טסון ננו והפעלה מהירה עבור הדגמה של שני ראייה: 4 שלבים

ביטול הארגז של ג'טסון ננו והפעלה מהירה עבור הדגמה של שני חזון: סיכום כפי שאתה יודע, ג'טסון ננו הוא כעת מוצר כוכב. והיא יכולה לפרוס בהרחבה טכנולוגיית רשת עצבית למערכות משובצות. להלן מאמר שאינו מתארז עם פרטי המוצר, תהליך ההפעלה ושתי הדגמות חזותיות … ספירת מילים: 800
השתמש בקלט אנלוגי אחד עבור 6 לחצנים עבור Arduino: 6 שלבים
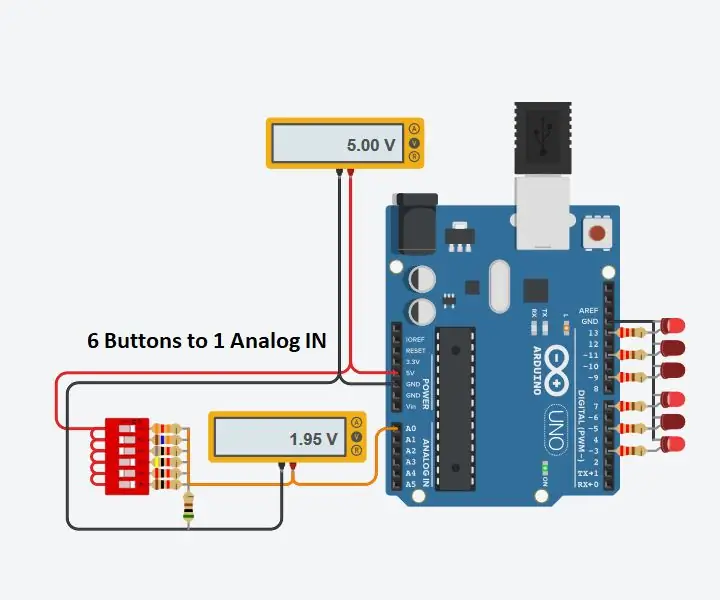
השתמש בכניסת אנלוגית אחת ל -6 לחצנים עבור Arduino: לעתים קרובות תהיתי כיצד אוכל להשיג יותר כניסות דיגיטליות עבור Arduino שלי. לאחרונה עלה בדעתי שאני אמור להיות מסוגל להשתמש באחת הכניסות האנלוגיות להבאת מספר כניסות דיגיטליות. עשיתי חיפוש מהיר ומצאתי היכן אנשים נמצאים
תאורת LED מהירה, מהירה, זולה ומראה טוב (לכל אחד): 5 שלבים (עם תמונות)

מהיר, מהיר, זול, נראה טוב תאורת LED (לכל אחד): ברוכים הבאים לכולם :-) זו ההנחיה הראשונה שלי אז הערות יתקבלו בברכה :-) מה שאני מקווה להראות לכם הוא כיצד ליצור תאורת LED מהירה הנמצאת על מה שאתה צריך: כבלים LEDs נגדים (510 אוהם ל -12 וולט) מדבקים מגהץ מגהצים חותכים ושאר יסודות
