סיכום מערך רקורסיבי בג'אווה: 9 שלבים

2024 מְחַבֵּר: John Day | [email protected]. שונה לאחרונה: 2024-01-30 09:13

רקורסיה היא הליך שימושי מאוד ויעיל בזמן שיכול לפתור בעיה במהירות עם מעט מאוד קוד. רקורסיה כרוכה בשיטה שאתה יוצר המכנה את עצמו מקצר את הבעיה המקורית.

בדוגמה זו, נסכם מערך של 10 מספרים שלמים, אך הגודל יכול להיות בכל אורך.

אספקה

עליך לדעת תחביר ג'אווה בסיסי ולהיות עם ה- IDE שלך או עורך טקסט כדי לכתוב את הקוד שלך למשימה זו.

שלב 1: הגדר את השיטה העיקרית שלך

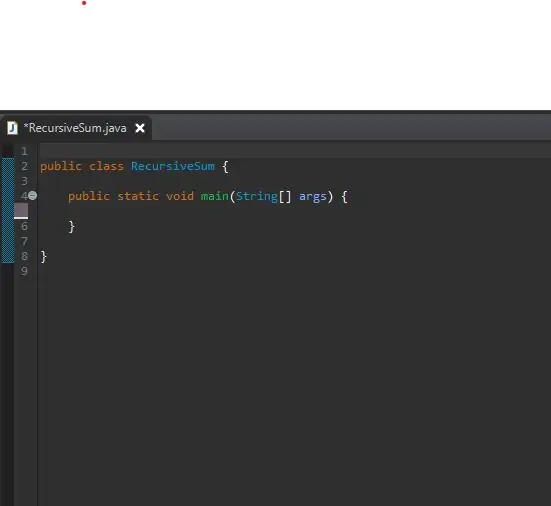
כדי להתחיל, הגדר את השיטה העיקרית שלך בכיתה חדשה שנוצרה. כיניתי את הכיתה שלי RecursiveSum. כאן תיצור את מערך המספרים השלמים ותקרא לשיטה הרקורסיבית שלך.

שלב 2: צור את כותרת השיטה הרקורסיבית שלך

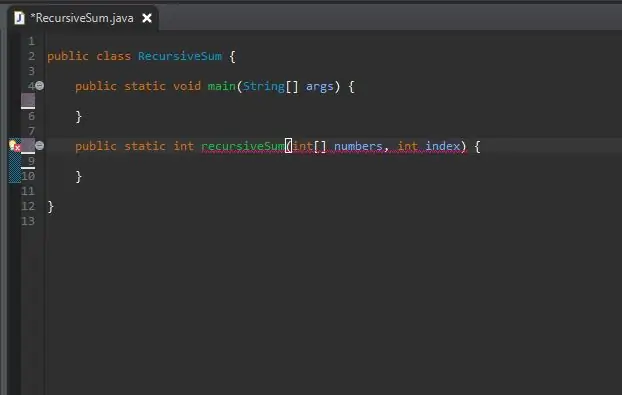
מחוץ לשיטה העיקרית שלך, צור את כותרת השיטה לשיטה הרקורסיבית שלך.

השיטה היא סטטית, מכיוון שהיא לא תדרוש מאובייקט להשתמש בה.

סוג ההחזרה הוא int, מכיוון שהמערך בו נשתמש יהיה מלא במספרים שלמים. עם זאת, ניתן לשנות זאת לכל סוג המספר שהמערך מכיל.

קראתי לשיטה שלי recursiveSum שתקבל שני פרמטרים; מערך של מספרים שלמים והאינדקס שנוסיף לסכום. התקשרתי לפרמטרים האלה למספרים ולאינדקס בהתאמה.

תראה שגיאות כרגע וזה בסדר. הם יתוקנו בהמשך.

שלב 3: צור את ה- Kicker/Base Case שלך

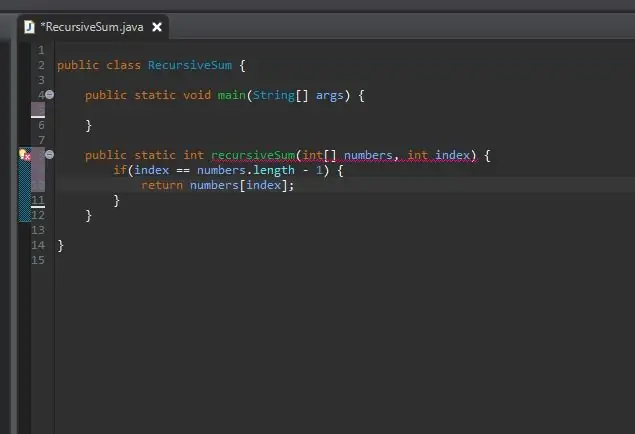
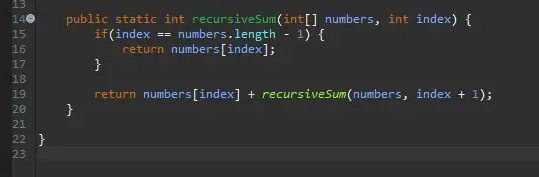
שיטה רקורסיבית צריכה מארז בעיטה/בסיס. זהו המצב שיעצור את השיטה שלך מלהתקשר אל עצמה אינסופית. ניתן לחשוב על מקרה בסיסי זה כמקרה הפשוט ביותר שנתקל בו. במקרה זה, מקרה הבסיס יהיה כאשר אנו נמצאים בקצה המערך שלנו. אם המדד הנוכחי שווה את אורך המערך (מינוס 1 מכיוון שמערכים מתחילים לספור מ -0 לא 1), אנחנו בסוף ואנחנו פשוט מחזירים את האלמנט הזה במדד זה.

שלב 4: השלב הרקורסיבי

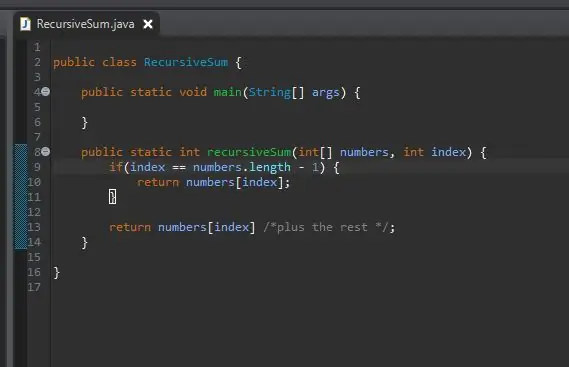
ברגע שיש לנו את מקרה הבסיס שלנו, השלב הבא הוא הצעד הרקורסיבי שלנו. כאן קורה הקסם. טיפלנו במקרה כשהמדד שלנו שווה לרכיב האחרון במערך שלנו. מה אם איננו ברכיב האחרון במערך שלנו? מה אם היינו יכולים פשוט להגיד לו להוסיף את האלמנט הנוכחי שלנו ואת הבא? בסופו של דבר נגיע לקצה המערך שלנו והתיק הבסיסי שלנו ישפיע.

לשם כך אנו פשוט מחזירים את האינדקס הנוכחי שלנו ו"מוסיפים את שאר "המערך.

שלב 5: קיצור הבעיה

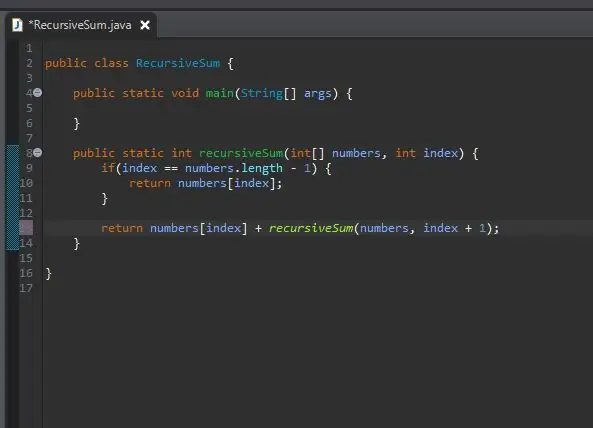
איך פשוט "מוסיפים את השאר"? יש לנו כבר שיטה שתוסיף אלמנט מסוים; שיטת recursiveSum () שלנו! אנחנו יכולים לקרוא לזה שוב אבל לשנות איזה אינדקס אנחנו מסכמים.

אנו עוברים באותו מערך שאנו מעבדים, אך אנו מעבירים את האינדקס הבא מהאינדקס הנוכחי שלנו. אנו עושים זאת על ידי הוספת אחת למדד הנוכחי שלנו כפי שמוצג.

שלב 6: צור מערך של שלמים

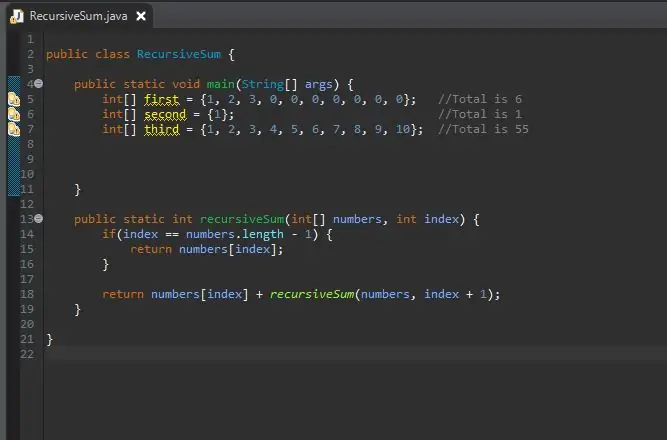
כעת, לאחר ששיטת הסיכום הרקורסיבית שלנו הושלמה, אנו יכולים ליצור את המערך שלנו אותו נעבוד. מערך זה יהיה בגוש השיטות העיקרי שלנו.

אתה יכול להפוך את גודל המערך לכל זמן שתרצה. יצרתי כמה מערכים שונים עם גדלים וערכים שונים כדי להראות שזה עובד לא רק על גודל אחד.

שלב 7: התקשר לשיטה עם המערכים שלך

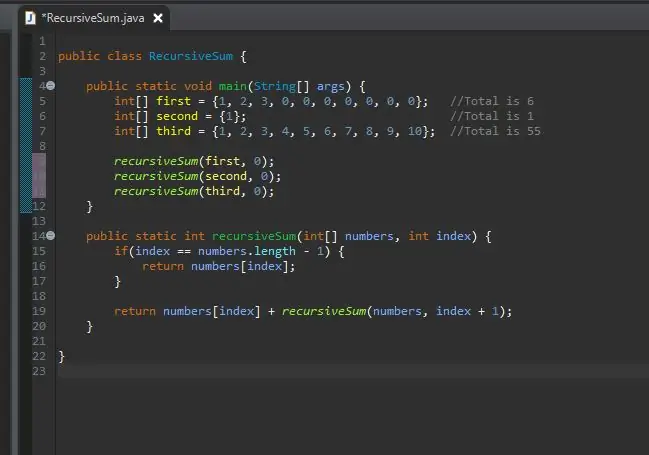
כעת תוכל להתקשר לשיטה הרקורסיבית שלך ולהעביר אליה את המערכים האלה. עכשיו אתה יכול להריץ את התוכנית שלך.

שלב 8: הדפס את התוצאות

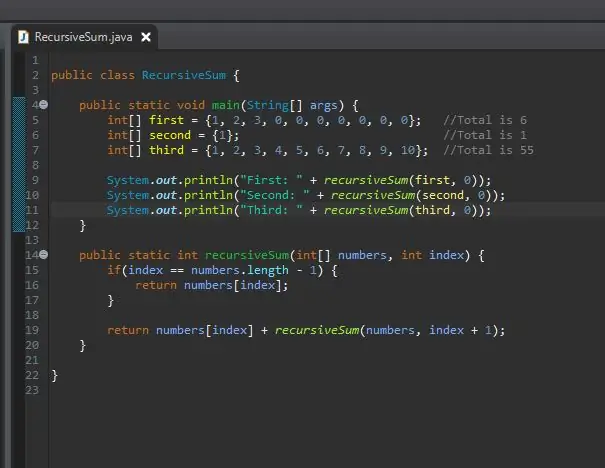
שום דבר לא קרה. למה? סכום רקורסיבי מחזיר מספר שלם אך לא עשינו דבר עם מספר שלם זה. זה עשה את העבודה שלו אבל אנחנו לא יכולים לראות את התוצאה. כדי לראות את התוצאה, אנו פשוט מדפיסים אותה כך. לאחר הפעלת זה אתה אמור לראות את התוצאות עבור כל אחד מהמערכים שלך.

שלב 9: מזל טוב

סיימת פונקציה רקורסיבית. אל תהסס לשנות את גודל המערכים שלך. אם תבדוק את זה, תבחין שהוא קורס כאשר יש לך מערך ריק. לא אחראי על זה אבל זו דרך מצוינת לשפר את השיטה הרקורסיבית שלך.