רובוט איזון עצמי באמצעות אלגוריתם PID (STM MC): 9 שלבים

2024 מְחַבֵּר: John Day | [email protected]. שונה לאחרונה: 2024-01-30 09:16

לאחרונה נעשתה עבודה רבה באיזון עצמי של אובייקטים. הרעיון של איזון עצמי החל באיזון של מטוטלת הפוכה. תפיסה זו הורחבה גם לעיצוב מטוסים. בפרויקט זה, עיצבנו מודל קטן של רובוט איזון עצמי באמצעות האלגוריתם PID (פרופורציונלי, אינטגרלי, נגזר). מאז, שיטה זו היא הפנים החדשות של מערכות בקרת התהליכים התעשייתיים. דו ח זה סוקר את השיטות הכרוכות באיזון עצמי של אובייקטים. פרויקט זה נערך כפרויקט סמסטר להבנת המתאם של PID על ההשפעה של תהליכים תעשייתיים שונים. כאן אנו מתמקדים רק במתן סקירה קצרה על האפקטיביות והיישום של בקרת ה- PID. מאמר זה פותח על ידי מתן היכרות קצרה עם מערכות בקרה וטרמינולוגיות נלוות, בנוסף למניעים לפרויקט. ניסויים ותצפיות נלקחו, יתרונות וחסרונות שתוארו עם סיום השיפורים העתידיים. מודל של רובוט איזון עצמי פותח כדי להבין את האפקטיביות של PID בעולם מערכת הבקרה. לאחר שעברתי כמה ניסויים קפדניים וניסויים, התגלו היתרונות והחסרונות של מערכת הבקרה ב- PID. נמצא כי למרות יתרונות רבים של שליטה ב- PID על שיטות קודמות, מערכת זו עדיין דורשת שיפורים רבים. יש לקוות שהקורא יקבל הבנה טובה של החשיבות של איזון עצמי, היעילות והחסרונות של שליטה ב- PID.

שלב 1: מבוא

עם הופעת המחשבים ותיעוש התהליכים, לאורך ההיסטוריה של האדם, תמיד היה מחקר לפיתוח דרכים לשיפור תהליכים וחשוב מכך, לשלוט בהם באמצעות מכונות באופן אוטונומי. המטרה היא להפחית את מעורבות האדם בתהליכים אלה, ובכך להפחית את הטעות בתהליכים אלה. מכאן שפותח תחום "הנדסת מערכות בקרה". ניתן להגדיר את הנדסת מערכות הבקרה כשימוש בשיטות שונות לשליטה על פעולתו של תהליך או תחזוקה של סביבה קבועה ומועדפת, בין אם היא ידנית או אוטומטית.

דוגמה פשוטה יכולה להיות שליטה על הטמפרטורה בחדר. שליטה ידנית פירושה נוכחות של אדם באתר הבודק את התנאים הנוכחיים (חיישן), משווה אותו לערך הרצוי (עיבוד) ונוקט בפעולה מתאימה להשגת הערך הרצוי (מפעיל). הבעיה בשיטה זו היא שהיא לא אמינה במיוחד מכיוון שאדם מועד לטעות או לרשלנות בעבודתו. כמו כן, בעיה נוספת היא שקצב התהליך שיזם המפעיל אינו תמיד אחיד, כלומר לפעמים הוא עלול להתרחש מהר מהנדרש או לעיתים הוא עשוי להיות איטי. הפתרון לבעיה זו היה שימוש בבקר מיקרו לשליטה במערכת. בקר הבקרה הוא

מתוכנת לשלוט בתהליך, על פי מפרט נתון, המחובר במעגל (עליו נדון בהמשך), הזן את הערך או את התנאים הרצויים ובכך שולט בתהליך כדי לשמור על הערך הרצוי. היתרון של תהליך זה הוא שאין צורך בהתערבות אנושית בתהליך זה. כמו כן, קצב התהליך אחיד

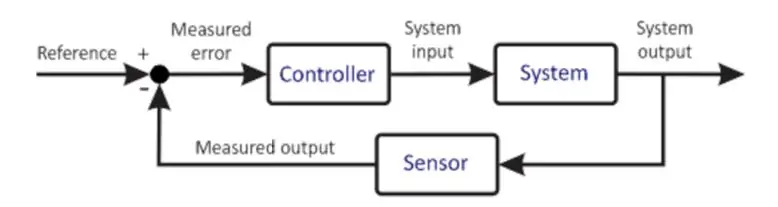
מערכת בקרה בסיסית

התרשים הקודם מציג גרסה פשוטה מאוד של מערכת בקרה. המיקרו -בקר הוא לב ליבה של כל מערכת בקרה. זהו מרכיב חשוב מאוד, לכן בחירת הבחירה שלה צריכה להיעשות בקפידה על סמך דרישות המערכת. בקר הבקרה מקבל קלט מהמשתמש. קלט זה מגדיר את המצב הרצוי של המערכת. בקר הבקרה מקבל גם קלט משוב מהחיישן. חיישן זה מחובר לפלט המערכת, שמידעו מועבר לקלט. המיקרו -מעבד, המבוסס על התכנות שלו, מבצע חישובים שונים ונותן פלט למפעיל. המפעיל, המבוסס על התפוקה, שולט במפעל כדי לנסות לשמור על תנאים אלה. דוגמה יכולה להיות נהג מנוע הנוסע במנוע שבו הנהג המנוע הוא המפעיל והמנוע הוא המפעל. המנוע, כך מסתובב במהירות נתונה. החיישן המחובר קורא את מצב המפעל כרגע ומזין אותו בחזרה לבקר המיקרו. בקר הבקרה שוב משווה, מבצע חישובים ובכך, המחזור חוזר על עצמו. תהליך זה חוזר על עצמו ואינסופי לפיו הבקר המיקרו שומר על התנאים הרצויים

שלב 2: מערכת בקרה מבוססת PID

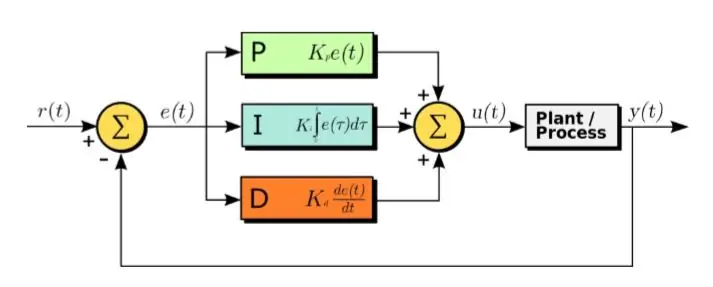
אלגוריתם ה- PID הוא שיטה יעילה לתכנון מערכת בקרה.

הגדרה

PID מייצג פרופורציונאלי, אינטגרלי ונגזרת. באלגוריתם זה, אות השגיאה המתקבל הוא הקלט. והמשוואה הבאה מוחלת על אות השגיאה

U (t) = Kp ∗ e (t) + Kd ∗ d/dt (e (t)) + Ki ∗ אינטגרל (e (t)) (1.1)

הסבר קצר

כפי שניתן לראות במשוואה לעיל, האינטגרל והנגזרת של אותות השגיאה מחושבים, מוכפלים עם הקבועים שלהם ומתווספים יחד עם Kp הקבוע כפול e (t). הפלט מוזר לאחר מכן למפעיל שגורם למערכת לפעול. עכשיו בואו נסתכל על כל חלק של הפונקציה בתורו. פונקציה זו משפיעה ישירות על זמן העלייה, זמן הנפילה, השיא מעל הצילומים, זמן ההתיישבות וטעות במצב יציב.

• חלק פרופורציונאלי: החלק הפרופורציוני מקטין את זמן העלייה ומקטין את שגיאת המצב היציב. המשמעות היא שלמערכת ייקח פחות זמן להגיע לשיא השיא שלה וכאשר תגיע למצב יציב, שגיאת המצב היציב תהיה נמוכה. עם זאת, הוא מגדיל את שיא החריגה.

• חלק נגזר: החלק הנגזר מקטין את מעבר החירום ואת זמן ההתיישבות. המשמעות היא שהמצב החולף של המערכת יהיה רטוב יותר. כמו כן, המערכת תגיע למצבה היציב תוך פחות זמן. עם זאת, אין לזה השפעה על זמן העלייה או על שגיאת המצב היציב.

• חלק אינטגרלי: החלק האינטגרלי מקטין את זמן העלייה ומונע לחלוטין את שגיאת המצב היציב. עם זאת, הוא מגדיל את שיא החריגה ואת זמן ההתיישבות.

• כוונון: מערכת בקרה טובה תהיה בעלת זמן עלייה נמוך, זמן יישוב, שיא יתר ושיטור מצב יציב. לכן יש לכוונן היטב את Kp, Kd, Ki כדי להתאים את התרומה של הגורמים הנ ל כדי לרכוש מערכת בקרה טובה.

צורפה איור המראה את ההשפעה של שינוי פרמטרים שונים באלגוריתם PID.

שלב 3: רובוט איזון עצמי

רובוט איזון עצמי הוא רובוט דו-גלגלי רב שכבתי.

הרובוט ינסה לאזן את עצמו על הפעלת כל כוח לא שווה. הוא יאזן את עצמו באמצעות הפעלת כוח המתנגד לתוצאה של הכוחות על הרובוט.

שיטות לאיזון עצמי

ישנן ארבע שיטות לאיזון עצמי של רובוטים. אלה הם כדלקמן:

איזון עצמי באמצעות שני חיישן הטיית IR

זוהי הדרך הגסה ביותר לאזן את הרובוט מכיוון שהוא דורש פחות חומרה ואלגוריתם קל יחסית. בגישה זו, שני חיישני IR מוטים משמשים למדידת המרחק בין הקרקע לרובוט. בהתבסס על המרחק המחושב, ניתן להשתמש ב- PID כדי להניע את המנועים לאזן את הרובוט בהתאם. חסרון אחד של שיטה זו הוא שחיישן IR יכול לפספס כמה קריאות. בעיה נוספת היא שנדרשת הפסקה ולולאות לחישוב המרחק מה שמגדיל את מורכבות הזמן של האלגוריתם. מכאן ששיטה זו לאיזון הרובוט אינה יעילה במיוחד.

איזון עצמי באמצעות מד תאוצה

מד תאוצה נותן לנו את האצת הגוף ב -3 צירים. האצה הממוקמת בציר y (כלפי מעלה) וציר ה- x (קדימה) נותנת לנו את המדד לחישוב כיוון הכבידה ומכאן לחשב את זווית הנטייה. הזווית מחושבת כדלקמן:

θ = arctan (Ay/Ax) (1.2)

החיסרון בשיטה זו הוא שבמהלך תנועת הרובוט תתווסף ההאצה האופקית לקריאות שהם רעש בתדירות גבוהה. מכאן שזווית הנטייה לא תהיה מדויקת.

איזון עצמי באמצעות ג'ירוסקופ

ג'ירוסקופ משמש לחישוב מהירות הזווית לאורך שלושת הצירים. זווית הנטייה מתקבלת באמצעות המשוואה הבאה.

θp (i) = θp (i − 1) + 1/6 (vali − 3 + 2vali − 2 + 2vali − 1 + vali) (1.3)

חיסרון אחד גדול בשימוש בג'ירוסקופ הוא שיש לו Bias DC קטן שהוא רעש בתדר נמוך ותוך כמה זמן הערכים המוחזרים שגויים לחלוטין. זה, לאחר האינטגרציה, יגרום לנקודת האפס להיסחף. כתוצאה מכך, הרובוט יישאר במיקום האנכי שלו למשך זמן מה ויפול לאחר שהסחף יגיע.

איזון עצמי באמצעות מד תאוצה וג'ירוסקופ כאחד

כפי שפורט לעיל, שימוש רק במד תאוצה או בג'ירוסקופ לא ייתן לנו את זווית הנטייה הנכונה. לשם כך משתמשים במד תאוצה ובג'ירוסקופ. שניהם מוטבעים ב- MPU6050. בכך אנו מקבלים את הנתונים משניהם ולאחר מכן ממיסים אותם באמצעות מסנן קלמן או מסנן משלים.

• מסנן קלמן: פילמן קלמן מחשב את האומדן הטוב ביותר של מצב מערכת דינאמית מתוך מדידות רועשות, וממזער את הטעות הממוצעת בריבוע של האומדן. הוא פועל בשני שלבים, חיזוי ותיקון, בהתחשב במשוואות הסטוכסטיות הנפרדות המתארות את דינמיקת המערכת. עם זאת, זהו אלגוריתם מורכב מאוד ליישום במיוחד על חומרה מוגבלת של מיקרו -בקר.

• מסנן משלים: אלגוריתם זה משתמש בעיקר בנתונים המתקבלים מהג'ירוסקופ ומשלב אותו לאורך זמן כדי לקבל את זווית הנטייה. הוא משתמש גם בחלק קטן מהקריאות של מד התאוצה. פילטר משלים, למעשה, ממזער את רעש התדר הגבוה של מד התאוצה ואת רעש התדר הנמוך של הג'ירוסקופ ואז ממיס אותם כדי לתת את זווית הנטייה המדויקת הטובה ביותר.

שלב 4: עיצוב הרובוט

עיצבנו רובוט איזון עצמי באמצעות בקר נגזר פרופורציונלי המיושם על ידי מסנן משלים עבור MPU6050. מודל קטן זה של רובוט איזון עצמי ימחיש לנו את התועלת של מערכות בקרה באיזון עצמי של רובוטים.

הטמעת מערכת:

המערכת היא רובוט איזון עצמי. הוא מיושם באמצעות בקר PID שהוא בקר נגזר אינטגרלי פרופורציונלי. אנו מאזנים את הרובוט על ידי הנעה בגלגליו לכיוון נפילתו. בכך אנו מנסים לשמור על מרכז הכובד של הרובוט מעל נקודת הציר. כדי להניע את הגלגלים לכיוון נפילתו, עלינו לדעת היכן נופל הרובוט ומהירות נפילתו. נתונים אלה מתקבלים באמצעות MPU6050 בעל מד תאוצה וג'ירוסקופ. MPU6050 מודד את זווית הנטייה ונותן את הפלט שלה לבקר המיקרו. MPU6050 מתממשק עם לוח STM באמצעות I2C. ב- I2C, חוט אחד מיועד לשעון הנקרא SCL. השני מיועד להעברת נתונים שהיא SDA. בכך משתמשים בתקשורת אב עבדים. כתובת ההתחלה וכתובת הסיום מוגדרת כדי לדעת מהיכן הנתונים מתחילים והיכן הם מסתיימים. יישמנו כאן את המסנן המשלים עבור MPU6050 שהוא פילטר מתמטי למיזוג התפוקות של מד תאוצה וג'ירוסקופ. לאחר קבלת הנתונים מ- MPU6050, המיקרו -בקר יבצע חישובים כדי לדעת היכן הוא נופל. בהתבסס על החישובים, מיקרו-בקר STM ייתן פקודות לנהג המנוע להסיע את הרכבים לכיוון נפילה אשר יאזן את הרובוט.

שלב 5: רכיבי הפרויקט

הרכיבים הבאים שימשו בפרויקט הרובוט לאיזון עצמי:

STM32F407

בקר מיקרו שתוכנן על ידי ST Microelectronics. זה עובד על ארכיטקטורת ARM Cortex-M.

נהג מנוע L298N

IC זה משמש להפעלת המנוע. הוא מקבל שתי כניסות חיצוניות. אחד מהמיקרו -בקר המספק לו אות PWM. על ידי התאמת רוחב הדופק, ניתן לכוון את מהירות המנוע. הכניסה השנייה שלו היא מקור המתח הנדרש להנעת המנוע שהיא סוללת 12V במקרה שלנו.

מנוע DC

מנוע DC פועל על אספקת DC. בניסוי זה, מנוע DC פועל באמצעות מחברי האופטוקלים המחוברים לנהג המנוע. כדי להניע את המנוע השתמשנו ב- Motor Drive L298N.

MPU6050

MPU6050 משמש לקבלת המידע על המקום בו הרובוט נופל. הוא מודד את זווית הנטייה ביחס לנקודת הנטייה האפסית שהיא המיקום של MPU6050 כאשר התוכנית מתחילה לפעול.

ל- MPU6050 יש תאוצה 3 צירים וג'ירוסקופ 3 צירים. מד התאוצה מודד תאוצה לאורך שלושת הצירים והג'ירוסקופ מודד את קצב הזווית סביב שלושת הצירים. על מנת לשלב את הפלט, עלינו לסנן את הרעשים של שניהם. כדי לסדר את הרעשים, יש לנו קלמן ומסנן משלים. יישמנו פילטר משלים בפרויקט שלנו.

אופטו זוג 4N35

מצמד אופטי הוא מכשיר המשמש לבידוד חלק המתח הנמוך וחלק המתח הגבוה של המעגל. כפי שהשם מרמז, הוא פועל על בסיס אור. כאשר חלק המתח הנמוך מקבל אות, זרם זרם בחלק המתח הגבוה

שלב 6: מבנה הרובוט

מבנה הרובוט מוסבר כדלקמן:

מבנה פיזי

הרובוט לאיזון עצמי מורכב משתי שכבות המורכבות מזכוכית פלסטיק שקופה. להלן פירוט של שתי שכבות:

שכבה ראשונה

בחלק התחתון של השכבה הראשונה, הצבנו תא להפעלת לוח STM. כמו כן הונחו שני מנועים של 4 וולט כל אחד מכל צד עם צמיגים המחוברים לתנועה של הרובוט. בחלק העליון של השכבה הראשונה הוצבו שתי סוללות של 4 וולט כל אחת (8 וולט בסך הכל) ומנהג מנוע IC (L298N) להפעלת מנועים.

שכבה שנייה

בשכבה העליונה של הרובוט, הנחנו את לוח ה- STM על לוח Perf. לוח פרפ נוסף של 4 מצמדי אופטו מונח על השכבה העליונה. ג'ירוסקופ ממוקם גם על השכבה העליונה של הרובוט מהצד התחתון. שני המרכיבים ממוקמים בחלק האמצעי כך שמרכז הכובד יישאר נמוך ככל האפשר.

מרכז הכובד של הרובוט

מרכז הכובד נשמר נמוך ככל האפשר. לשם כך, הנחנו סוללות כבדות על השכבה התחתונה ורכיבים קלים כגון לוח STM ואופקטופולריים על השכבה העליונה.

שלב 7: קוד

הקוד נאסף ב- Atollic TrueStudio. סטודיו STM שימש למטרות ניפוי באגים.

שלב 8: סיכום

לאחר הרבה ניסויים והתבוננות, אנו מגיעים לבסוף למצב בו אנו מסכמים את תוצאותינו ודנים עד כמה הצלחנו ליישם ולעבד את האפקטיביות של המערכת.

סקירה כללית

במהלך הניסוי, מהירות המנוע נשלטה בהצלחה באמצעות אלגוריתם PID. אולם העקומה אינה בדיוק קו ישר חלק. יש לכך הרבה סיבות:

• החיישן, אף שהוא מחובר למסנן נמוך, עדיין מספק ירידות מסוימות מסוימות; אלה נובעים מהתנגדות לא לינארית וכמה סיבות בלתי נמנעות של האלקטרוניקה האנלוגית.

• המנוע אינו מסתובב בצורה חלקה תחת מתח קטן או PWM. הוא מספק טלטולים שעלולים לגרום לערכים שגויים המוזנים למערכת.

• בשל התנודדות, החיישן עלול לפספס כמה חריצים המספקים ערכים גבוהים יותר. • סיבה מרכזית נוספת לטעויות יכולה להיות תדירות שעון הליבה של בקר ה- mic mic. דגם זה של מיקרו -בקר STM מספק שעון ליבה של 168MHz. למרות שהתמודדו עם בעיה זו בפרויקט זה, קיימת תפיסה כללית לגבי מודל זה כי הוא אינו מספק תדירות כה גבוהה.

מהירות הלולאה הפתוחה מספקת קו חלק מאוד עם כמה ערכים לא צפויים בלבד. אלגוריתם ה- PID פועל גם כן, המספק זמן התיישבות נמוך מאוד של המנוע. אלגוריתם ה- PID של המנוע נבדק במתח שונה השומר על מהירות ההתייחסות קבועה. שינוי המתח אינו משנה את מהירות המנוע ומראה שאלגוריתם ה- PID עובד בסדר

אפקטיביות

כאן אנו דנים באפקטיביות של בקר ה- PID שראינו במהלך הניסוי.

יישום פשוט

ראינו בסעיף הניסויים והתצפיות כי קל מאוד ליישם בקר PID. זה דורש רק שלושה פרמטרים או קבועים שיש להגדיר על מנת שתהיה מערכת בקרת מהירות

יעילות ללא תחרות עבור מערכות לינאריות

בקר PID לינארי הוא החשוב ביותר במשפחת הבקרים מכיוון שההיגיון פשוט מאוד והיישום נפוץ במקרה של יישומים ליניאריים או לינאאריים למדי.

מגבלות

הסברנו בתקציר על המגבלות של מערכת זו. כאן אנו דנים בכמה מהם שראינו.

בחירת קבועים

ראינו כי למרות שקל ליישם בקר PID, עדיין זהו חסרון משמעותי במערכת כי שלב בחירת ערך הקבועים הוא מאמץ; כיוון שצריך לבצע חישובים קשים. הדרך האחרת היא שיטת הניסוי והניסיון, אך גם היא לא יעילה.

קבועים לא תמיד קבועים

תוצאות הניסוי הראו כי עבור ערכים שונים של מהירות ההתייחסות של המנוע, בקר ה- PID לא תקין עבור אותם ערכים של קבועי ה- PID. למהירויות שונות, היה צריך לבחור את הקבועים באופן שונה וזה מעלה את העלות החישובית באופן אקספוננציאלי.

לא לינארי

בקר ה- PID המשמש במקרה שלנו הוא לינארי, ולכן ניתן ליישמו על מערכות לינאריות בלבד. עבור מערכות לא לינאריות, הבקר צריך להיות מיושם באופן שונה. למרות שישנן שיטות לא לינאריות שונות של PID, הן דורשות בחירת פרמטרים נוספים. זה שוב הופך את המערכת לבלתי רצויה בגלל עלות חישובית גבוהה.

דחיפה ראשונית נדרשת

הראינו בחלק הניסויים כי עבור מהירות התייחסות קטנה למדי שבה השגיאה קטנה למדי בהתחלה, ה- PWM המסופק על ידי ה- PID הוא כל כך קטן שהוא אינו מייצר את מומנט ההתחלה הנדרש עבור המנוע. כך שהמנוע בחלק מהניסויים אינו פועל או בניסויים אחרים מספק מעבר גדול וזמן התיישבות ארוך יותר.

שלב 9: תודה מיוחדת

תודה מיוחדת לחברי הקבוצה שעזרו לי לעבור את הפרויקט הזה.

בקרוב אעלה את הקישור לסרטון.

אני מקווה שזה מעניין אותך.

זהו טאהיר אול האק מ- UET החתום. לחיים !!!