
- מְחַבֵּר John Day day@howwhatproduce.com.
- Public 2024-01-30 09:16.
- שונה לאחרונה 2025-01-23 14:46.



במדריך זה אני הולך להראות לך כיצד לבנות משחק Tic Tac Toe עם AI באמצעות Arduino. אתה יכול לשחק נגד הארדואינו או לצפות בארדואינו משחק נגד עצמו.
אני משתמש באלגוריתם שנקרא "אלגוריתם מינימקס", שניתן להשתמש בו לא רק לבניית AI עבור Tic Tac Toe, אלא גם למגוון משחקים אחרים כמו Four in a Row, דמקה או אפילו שחמט. משחקים כמו שחמט הם מורכבים מאוד ודורשים גרסאות מעודנות הרבה יותר של האלגוריתם. למשחק Tic Tac Toe שלנו, אנו יכולים להשתמש בגרסה הפשוטה ביותר של האלגוריתם, אשר בכל זאת די מרשים. למעשה, ה- AI כל כך טוב שאי אפשר לנצח את הארדואינו!
המשחק קל לבנייה. אתה צריך רק כמה מרכיבים והשרטוט שכתבתי. הוספתי גם הסבר מפורט יותר של האלגוריתם, אם אתה רוצה להבין איך זה עובד.
שלב 1: בנה ושחק
כדי לבנות את משחק הטיק טק תצטרך את הרכיבים הבאים:
- אונו ארדואינו
- 9 נוריות WS2812 RGB
- 9 כפתורי לחיצה
- כמה כבלי חוט ומגשר
חבר את הרכיבים כפי שמוצג בסקיצה של פריטינג. לאחר מכן העלה את הקוד ל- Arduino שלך.
כברירת מחדל, ה- Arduino לוקח את הסיבוב הראשון. כדי להפוך את הדברים למעניינים יותר, המהלך הראשון נבחר באופן אקראי. לאחר המהלך הראשון, Arduino משתמש באלגוריתם המינימקס כדי לקבוע את המהלך הטוב ביותר האפשרי. אתה מתחיל משחק חדש על ידי איפוס ה- Arduino.
אתה יכול לצפות ב"חשיבה "של Arduino על ידי פתיחת הצג הסידורי. עבור כל מהלך אפשרי, האלגוריתם מחשב דירוג המציין אם מהלך זה יוביל לזכייה (ערך 10) או הפסד (ערך -10) עבור הארדואינו או תיקו (ערך 0).
אתה יכול גם לצפות בארדואינו משחק נגד עצמו על ידי ביטול התגובה לשורה "#define DEMO_MODE" ממש בתחילת המערכון. אם אתה מעלה את הסקיצה שהשתנתה, הארדואינו מבצע את הצעד הראשון באופן אקראי ולאחר מכן משתמש באלגוריתם המינימקס כדי לקבוע את המהלך הטוב ביותר עבור כל שחקן בכל סיבוב.
שים לב שאתה לא יכול לנצח נגד הארדואינו. כל משחק יסתיים בתיקו או שתפסיד אם תעשה טעות. הסיבה לכך היא שהאלגוריתם תמיד בוחר את המהלך הטוב ביותר האפשרי. כפי שאולי אתם יודעים, משחק של טיק טוק טו תמיד יסתיים בתיקו אם שני השחקנים לא יטעו. במצב הדגמה, כל משחק מסתיים בתיקו מכיוון שכפי שכולנו יודעים, מחשבים לעולם אינם טועים;-)
שלב 2: האלגוריתם המינימקס

האלגוריתם מורכב משני מרכיבים: פונקציית הערכה ואסטרטגיית חיפוש. פונקציית ההערכה היא פונקציה המקצה ערך מספרי לעמדות הלוח. אם העמדה היא עמדה סופית (כלומר, עמדה שבה השחקן הכחול או השחקן האדום זכו או שאף אחד מהשחקנים לא זכה), פונקציית ההערכה היא פשוטה מאוד: נניח שהארדואינו משחק כחול והשחקן האנושי משחק אדום. אם המיקום הוא מיקום מנצח עבור כחול, הפונקציה מקצה ערך למיקום זה 10; אם מדובר במיקום מנצח באדום, הפונקציה מייחסת למיקום ערך של -10; ואם המיקום הוא תיקו, הפונקציה מקצה ערך של 0.
כאשר הגיע תורו של הארדואינו, הוא רוצה לבחור מהלך שממקסם את הערך של פונקציית ההערכה, מכיוון שמקסום הערך פירושו שהוא יעדיף ניצחון על תיקו (10 גדול מ -0) ויעבור תיקו על הפסד (0 גדול מ -10). על ידי טיעון מקביל, היריבה רוצה לשחק בצורה כזו שהיא ממזערת את הערך של פונקציית ההערכה.
למיקום שאינו סופי, האלגוריתם מחשב את הערך של פונקציית ההערכה על ידי אסטרטגיית חיפוש רקורסיבית. החל מהמיקום הנוכחי, הוא מדמה לסירוגין את כל המהלכים שהשחקן הכחול והשחקן האדום יכולים לבצע. ניתן לדמיין זאת כעץ, כמו בתרשים. כאשר הוא מגיע למיקום סופי, הוא מתחיל לחזור אחורה, כשהוא נושא את ערך פונקציית ההערכה מרמת החזר הנמוכה לרמת החזר הגבוהה יותר. הוא מקצה את המקסימום (אם בשלב החזר המתאים תורו של השחקן הכחול) או המינימום (אם בשלב החזר המתאים תורו של השחקן האדום) לערכי פונקציית ההערכה מרמת החזר התחתונה למיקום על רמת רקורסיה גבוהה יותר. לבסוף, כאשר האלגוריתם סיים לחזור אחורה והגיע שוב למיקום הנוכחי, הוא לוקח את המהלך (או אחד המהלכים) שיש לו את ערך פונקציית ההערכה המרבית.
זה אולי נשמע קצת מופשט, אבל זה בעצם לא כל כך קשה. שקול את המיקום המוצג בחלק העליון של התרשים. בשלב החזר הראשון, ישנם שלושה מהלכים שונים שכחול יכול לבצע. כחול מנסה למקסם את הערך של פונקציית ההערכה. עבור כל אחד מהמהלכים הכחול יכול לבצע, ישנם שני מהלכים שאדום יכול לבצע. אדום מנסה למזער את הערך של פונקציית ההערכה. שקול את הצעד בו משחק כחול בפינה הימנית העליונה. אם האדום משחק בתיבה המרכזית, האדום ניצח (-10). אם, לעומת זאת, אדום משחק בתיבה התחתונה המרכזית, כחול ינצח בצעד הבא (10). לכן, אם כחול משחק בפינה הימנית העליונה, האדום ישחק בתיבה המרכזית, מכיוון שזה ממזער את הערך של פונקציית ההערכה. באופן אנלוגי, אם כחול משחק בתיבה התחתונה המרכזית, האדום שוב ישחק בתיבה המרכזית מכיוון שזה ממזער את פונקציית ההערכה. אם, לעומת זאת, כחול משחק בתיבה המרכזית, לא משנה איזה מהלך אדום לוקח, כחול תמיד ינצח (10). מכיוון שכחול רוצה למקסם את פונקציית ההערכה, הוא ישחק בתיבה המרכזית, מכיוון שמיקום זה גורם לערך גדול יותר של פונקציית ההערכה (10) מאשר שני המהלכים האחרים (-10).
שלב 3: פתרון בעיות ושלבים נוספים
אם אתה לוחץ על כפתור ונורית LED שונה מזו המתאימה לכפתור נדלקת, כנראה שהתבלבלת בין החוטים בסיכות A0-A2 או 4-6, או שחיברת את הנורות בסדר הלא נכון.
שים לב גם שהאלגוריתם לא בהכרח תמיד בוחר במהלך שיאפשר לארדואינו לנצח כמה שיותר מהר. למעשה, הקדשתי זמן לניקוי באגים של האלגוריתם מכיוון שהארדואינו לא בחר מהלך שהיה מהלך מנצח. לקח לי זמן עד שהבנתי שבמקום זאת בחר במהלך המבטיח שהוא יזכה במהלך אחד אחר כך. אם תרצה, תוכל לנסות לשנות את האלגוריתם כך שהוא תמיד יעדיף מהלך מנצח על פני זכייה מאוחרת יותר.
הרחבה אפשרית של פרויקט זה תהיה שימוש באלגוריתם לבניית AI עבור 4x4 או אפילו 5x5 Tic Tac Toe. עם זאת, שים לב שמספר העמדות שהאלגוריתם צריך לבחון גדל במהירות רבה. יהיה עליך למצוא דרכים להפוך את פונקציית ההערכה לאינטליגנטית יותר על ידי הקמת ערכים לעמדות שאינן סופיות, בהתבסס על הסבירות שהעמדה טובה או רעה לשחקן המדובר. תוכל גם לנסות להפוך את החיפוש לאינטליגנטי יותר על ידי הפסקת החזרה מוקדמת אם מהלך פחות ראוי לחקירה נוספת מאשר מהלכים חלופיים.
ה- Arduino היא כנראה לא הפלטפורמה הטובה ביותר להרחבות כאלה בגלל הזיכרון המוגבל שלה. רקורסיה מאפשרת לערימה לצמוח במהלך ביצוע התוכנית, ואם הערימה גדלה יותר מדי, היא עלולה להשחית את זיכרון התוכנית, ולהוביל לקריסות או להתנהגות לא יציבה. בחרתי בארדואינו לפרויקט זה בעיקר בגלל שרציתי לבדוק אם אפשר לעשות זאת ולמטרות חינוכיות, לא כי זו הבחירה הטובה ביותר לבעיות מסוג זה.
מוּמלָץ:
רובוט איזון עצמי - אלגוריתם בקרת PID: 3 שלבים

רובוט איזון עצמי - אלגוריתם בקרת PID: פרויקט זה נבנה כי התעניינתי ללמוד עוד על אלגוריתמי בקרה וכיצד ליישם לולאות PID פונקציונליות ביעילות. הפרויקט עדיין בשלבי פיתוח מכיוון שטרם הוסיף מודול בלוטות 'אשר יביא
אלגוריתם קורדי באמצעות VHDL: 4 שלבים
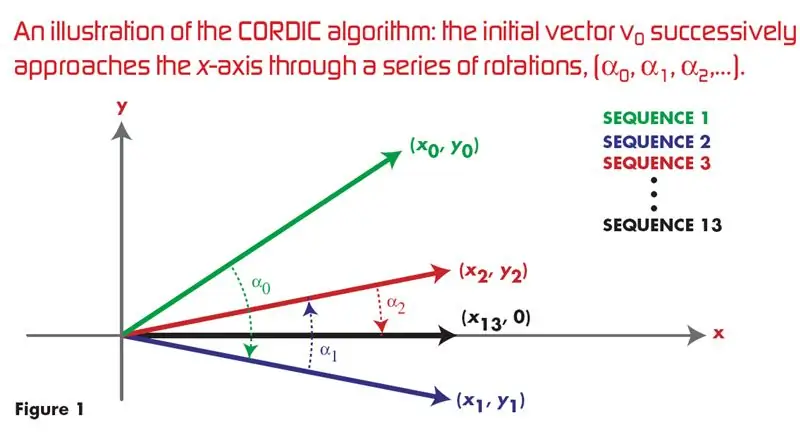
אלגוריתם קורדי באמצעות VHDL: ## זהו הקישור הפופולרי ביותר שנלחץ בגוגל ליישום VHDL של CORDIC ALGORITHM ליצירת גל סינוס וקוסינוס ## כיום קיימים אלגוריתמים יעילים בחומרה רבים, אך אלה אינם ידועים היטב בשל הדומיננטיות של המלחמה הרכה
Tic Tac Toe: 12 שלבים
Tic Tac Toe: היום נכין משחק Tic Tac Toe ב- TinkerCad באמצעות ה- Arduino. אנו הולכים להשתמש בהרבה רכיבים פשוטים ולהשתמש בקוד כדי לקשור את כולם יחד. החלק העיקרי במעגל זה שמאגד את כל זה הוא הקוד. הפרוג 'הזה
רובוט איזון עצמי באמצעות אלגוריתם PID (STM MC): 9 שלבים

רובוט איזון עצמי באמצעות אלגוריתם PID (STM MC): לאחרונה נעשתה עבודה רבה באיזון עצמי של אובייקטים. הרעיון של איזון עצמי החל באיזון של מטוטלת הפוכה. תפיסה זו הורחבה גם לעיצוב מטוסים. בפרויקט זה, עיצבנו מוד קטן
בקרת מהירות של מנוע DC באמצעות אלגוריתם PID (STM32F4): 8 שלבים (עם תמונות)

בקרת מהירות של מנוע DC באמצעות אלגוריתם PID (STM32F4): שלום לכולם, זהו tahir ul haq עם פרויקט אחר. הפעם זה STM32F407 בתור MC. זהו פרויקט סוף אמצע סמסטר. מקווה שאתה אוהב את זה. זה דורש הרבה מושגים ותיאוריה אז אנחנו נכנסים לזה קודם. עם הופעת המחשבים ו
