האם אתה יודע על התאמת ESP32 ADC ?: 29 שלבים

2024 מְחַבֵּר: John Day | [email protected]. שונה לאחרונה: 2024-01-30 09:15

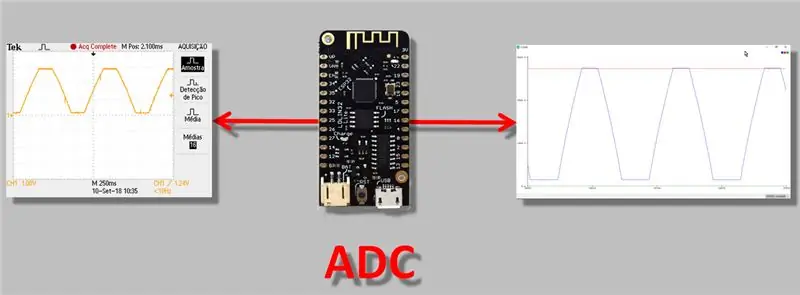
היום אני הולך לדבר על נושא טכני יותר, אבל נושא שלדעתי כל מי שעובד עם ESP32 צריך לדעת: סוגיית התאמת הקריאה של ADC (ממיר אנלוגי לדיגיטלי). אני חושב שזה חשוב מכיוון שכאשר אתה עושה "מדידה", במיוחד עם מכשיר בעל פלט אנלוגי, עליך להיות בטוח לחלוטין שהקריאה מתבצעת כהלכה.

לכן, בסרטון היום נבצע מדידות באמצעות "הממיר האנלוגי-דיגיטלי" של ה- ESP32, נצפה על פערי ההמרות וניישם שיטת התאמה / כיול ADC.

שלב 1: מהו ממיר AD?

ממיר AD הוא מעגל המסוגל לתרגם כמות אנלוגית (רציפה) לערכים דיגיטליים (בדיד). מה זה אומר? המשמעות היא שבעוד שערכים דיגיטליים יכולים להניח רק ערכים נפרדים הנוצרים משילוב של אפסים ואחד, כמות אנלוגית יכולה להניח כל ערך בתוך טווח. לדוגמה, אם מדדנו את המתח של תא AA אידיאלי, נוכל למצוא כל ערך בין 0V ל -1.5V, מכיוון שמדובר בכמות אנלוגית. מצב הפלט של מנורה אידיאלית חייב להניח רק שני מצבים (כבויים או דולקים), שהם בגודל דיסקרטי. מכיוון שבקרי מיקרו פועלים תוך שימוש בהיגיון דיסקרטי זה, אנו זקוקים למעגל המסוגל לתרגם כמות אנלוגית לדיגיטלית (או דיסקרטית).

שלב 2: שימוש במשאבים

• כרטיס Lolin32 Lite אחד v1.0.0

• אוסצילוסקופ Tektronix TDS1001C ללכידה

• כבל USB אחד ל- ESP32

• אוסצילוסקופ Hantek DSO4102C כמחולל אותות

שלב 3: ESP32 ADC

על פי נתוני Espressif, שבבי ESP32 עשויים להציג הבדל של +/- 6% משבב אחד לשני בתוצאות הנמדדות.

בנוסף, להמרה אין תשובה לינארית לכל טווח זמין לקריאה. Espressif מספקת שיטה לכיול ומציעה למשתמשים ליישם שיטות אחרות אם הם רואים צורך להשיג את הדיוק הרצוי.

נבצע רכישת נתונים, ומתוך כך נציג את תגובות ה- ADC ודוגמה ליישום תהליך מתמטי לקריאת ההתאמה.

ישנן מספר דרכים (פשוטות או מורכבות יותר) לביצוע התיקונים הללו. זה תלוי בך להעריך את המתאים ביותר לפרויקט שלך.

לזה שמוצג כאן תהיה מטרה ממחישה וינסה להתייחס לנקודות מעניינות שניתן לצפות בהן במהלך ההתאמות.

שלב 4: מעגל בשימוש

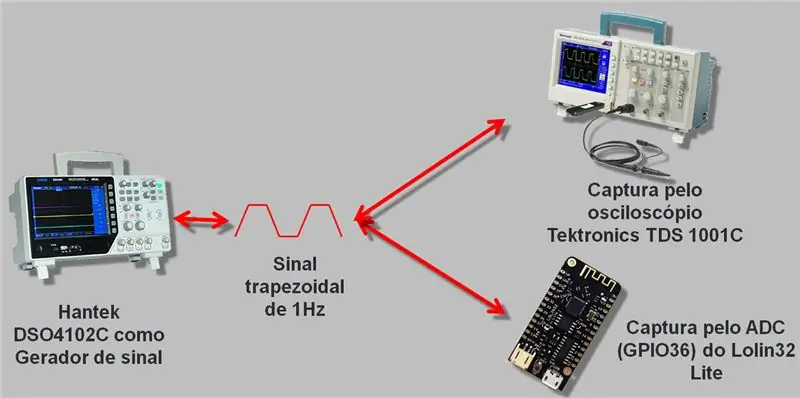
השתמשתי באוסילוסקופ עם מחולל אותות העולה עד 25 מגה -הרץ, ה- Hantek DSO4102C. יצרנו גל שנקרא על ידי ה- ESP A / D והאוסילוסקופ. הנתונים שנאספו נרשמו ב- csv ובגיליון אלקטרוני אותם אשאיר בסוף המאמר להורדה.

שלב 5: סימן בשימוש

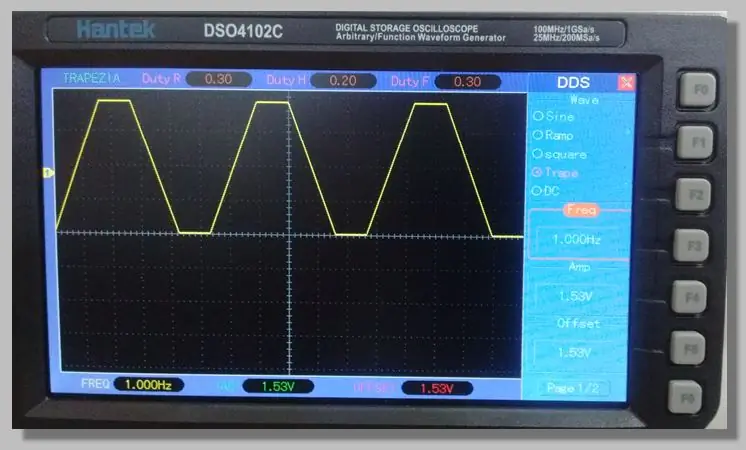
בחרנו באות טרפזי בתדר נמוך המאפשר גישה לרמפות העוברות בכל טווח ההמרות. זה מאפשר מספר רב של דגימות על רמפות אלה.

שלב 6: נתונים המתקבלים על ידי האוסילוסקופ

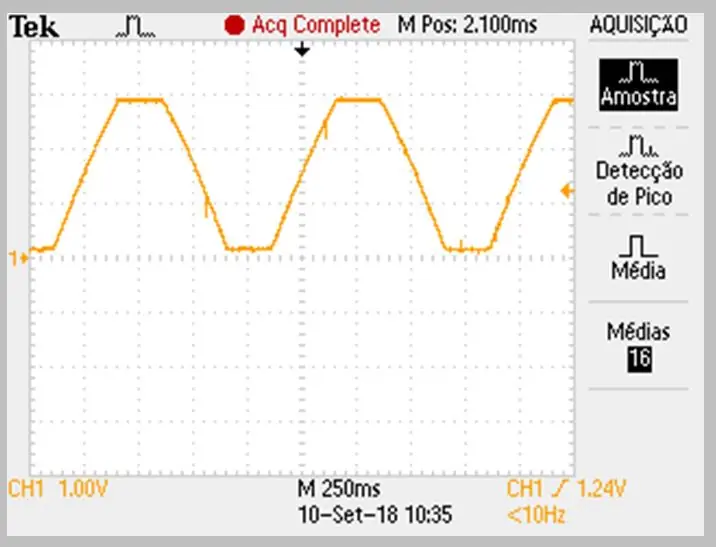
תמונת הלכידה בוצעה על ידי האוסילוסקופ. הנתונים נשמרו בקובץ csv. שימו לב לעקמומיות הקלה על הרמפות העולות והיורדות של האות.

שלב 7: נתונים המתקבלים על ידי האוסילוסקופ (קובץ csv ב- Excel)

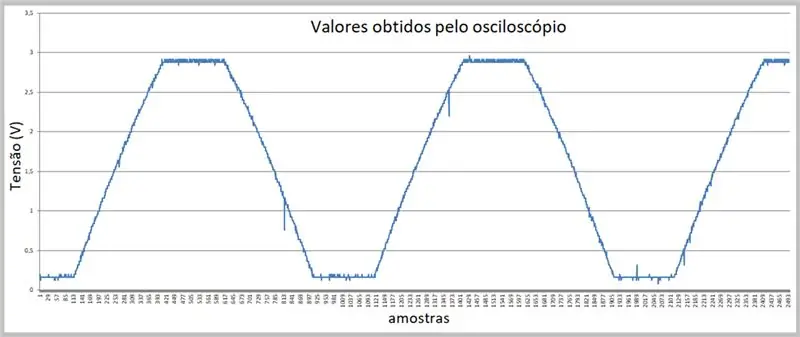
יש לנו את הדגימות כאן.

שלב 8: נתונים המתקבלים על ידי ה- ADC

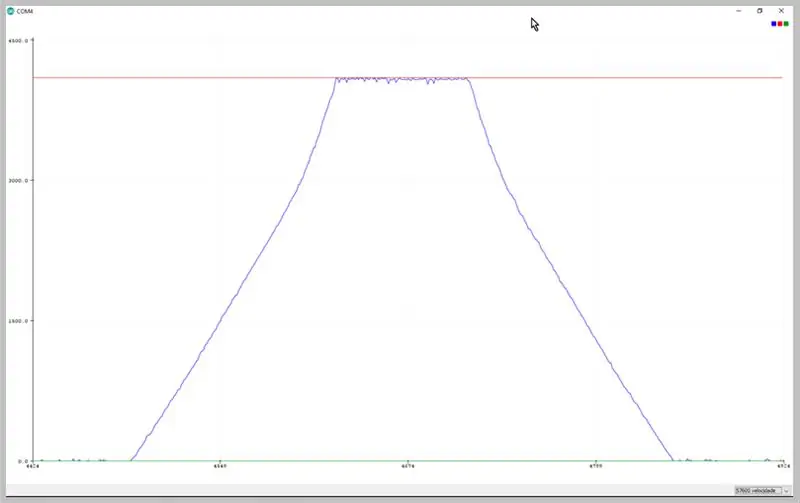
על ידי שינוי קצב ההעברה של הסדרה, נוכל לצפות בנתונים שנלכדו על ידי ה- ADC. שים לב לעיוות האות הטרפז.

נתונים שנצפו על פלוטר סידורי של Arduino IDE

שלב 9: נתונים המתקבלים על ידי ADC - Excel

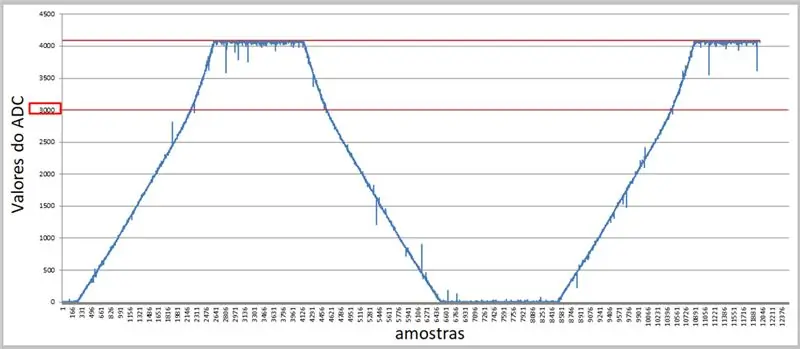
באמצעות תעריף גבוה יותר והמסוף הטורי, אנו יכולים ללכוד את הערכים וליישם אותם ב- Excel לצורך השוואותינו.

שלב 10: השוואה בין רמפות טיפוס

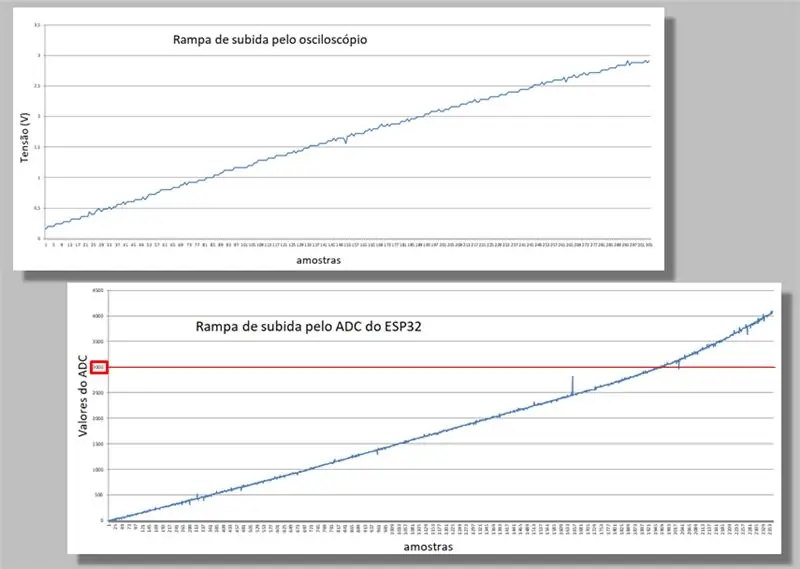
אנו משווים את שתי רמפות הטיפוס של שני המלכודות.

שימו לב לעקמומיות המתרחשת בשתי הרמפות.

שים לב גם שבאותה רמפה יש לנו הרבה יותר דוגמאות של ה- ESP32 מאשר מהאוסילוסקופ.

שלב 11: השוואת מספר הדגימות

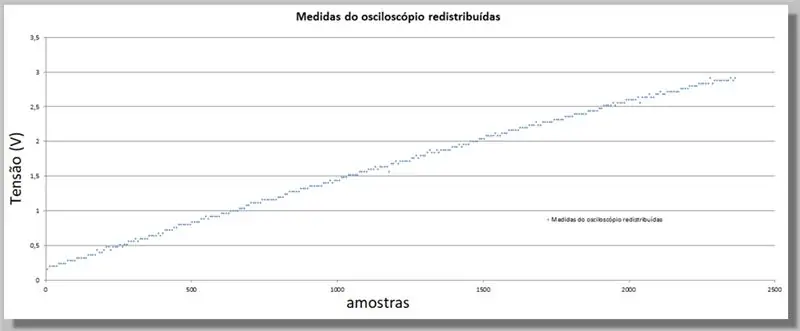
מכיוון ש- ESP32 סיפק מספר גדול יותר של דגימות מאשר האוסילוסקופ, עלינו להשוות ערכים אלה, מכיוון שהם ישמשו כמדד להשוואת שתי הקימורים.

לשם כך נבצע השוואה ישירה.

יש לנו 305 דגימות לרמפת האוסילוסקופ ו -2365 דגימות לרמפת ה- ADC.

מכיוון שהרמפות הן באותו טווח, אנו יכולים לומר שיש לנו כ- 7.75 דגימות של ה- ADC לכל אוסצילוסקופ.

להכפלת האינדקס של כל דגימת אוסצילוסקופ יש אותה עקומה, אך עם מדדים שווים ל- ADC ולנתונים המחולקים מחדש.

כדי למלא את הנתונים החסרים לתפקידים החדשים, ניישם עקומה המתאימה סטטיסטית לנתונים הידועים.

שלב 12: מילוי החסר - קו המגמה

בחירת הנתונים הידועים (נקודות כחולות), על ידי לחיצה ולאחר מכן לחיצה על הכפתור הימני, אנו בוחרים: "הוסף קו מגמה …"

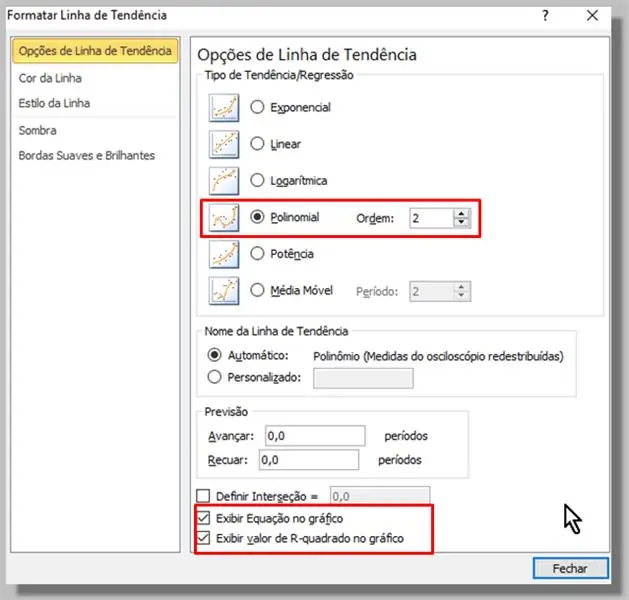
בחלון שמופיע, אנו בוחרים את סוג הפולינום (סדר 2 יספיק).

בדקנו גם את האפשרויות "הצג משוואה בתרשים" ו"הצג ערך בריבוע R בתרשים ".

אנו לוחצים על "סגור".

שלב 13: מילוי החסר - עקומת פולינום בדרגה 2

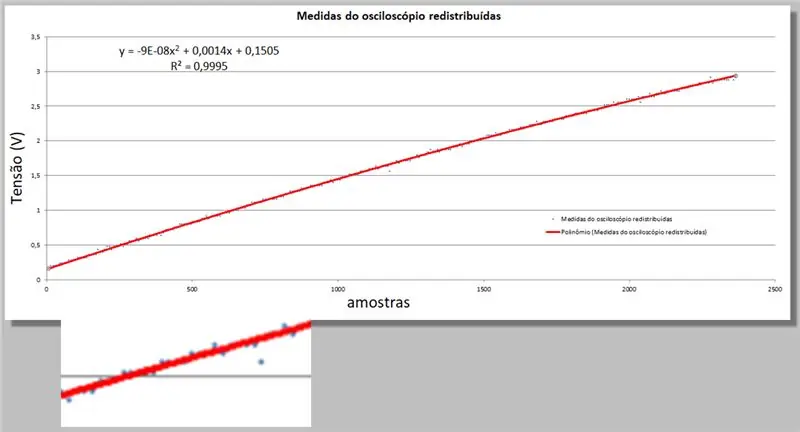
Excel מספק לנו שני פיסות מידע חדשות; משוואת הסדר השני המתאימה ביותר לנתונים, ומשוואת R בריבוע שמכמתת הלימות זו.

רק זכור שככל שקרוב יותר ל -1 המשוואה מתאימה יותר.

בואו לא נתעמק במתמטיקה הכרוכה בכך, בואו פשוט נשתמש בה ככלי.

שלב 14: מילוי החסר - הערכת הפונקציה

בואו למלא את פערי הדגימה בנתונים שנוצרים מהמשוואה. ואז, השווה אותם נקודה אחר נקודה.

y = -9E -08x2 + 0, 0014x + 0, 1505

R² = 0, 9999

מתח אוסצילוסקופ = -9E -08 * אינדקס 2 + 0, 0014 * אינדקס + 0, 1505

שלב 15: המרת מתח האוסילוסקופ לערך שווה ערך להשוואה ל- ADC

בואו ננצל זאת כדי להפוך גם את ערך מתח האוסילוסקופ לערך ADC שווה.

מכיוון שהערך הגבוה ביותר שהתקבל ב- ADP של ESP32 היה 4095, המקביל לקריאה של 2.958V לאותו מדד, אנו יכולים לומר כי:

כל וולט במדידות האוסילוסקופ שווה בערך ל- 1384.4 יחידות AD. לכן, אנו יכולים להכפיל את כל המדידות של האוסילוסקופ בערך זה.

שלב 16: השוואת שתי הרמפות המתקבלות

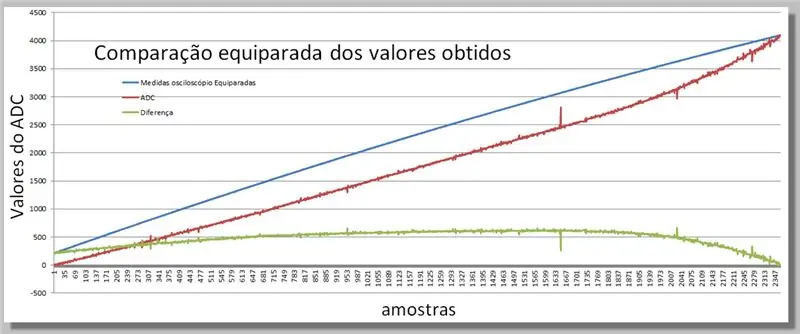
ויזואליזציה של ההבדלים המתקבלים בשתי הקריאות.

שלב 17: התנהגות הפרש הקריאה ב- ADC (ERROR)

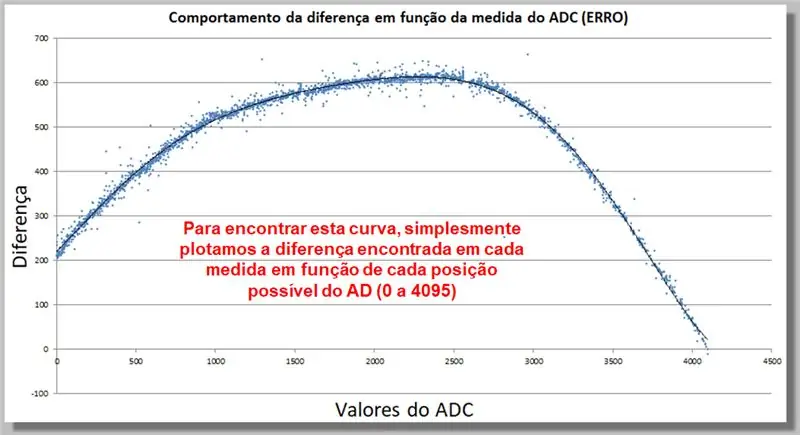
העקומה להלן מראה כיצד ההבדל בקריאת ADC מתנהג כפונקציה של המדידה. איסוף נתונים זה יאפשר לנו למצוא פונקציית תיקון.

כדי למצוא עקומה זו, אנו פשוט משרטטים את ההבדל הנמצא בכל מדד כפונקציה של כל מיקום AD אפשרי (0 עד 4095).

שלב 18: התנהגות ההבדל בקריאת ADC - מציאת פונקציית תיקון

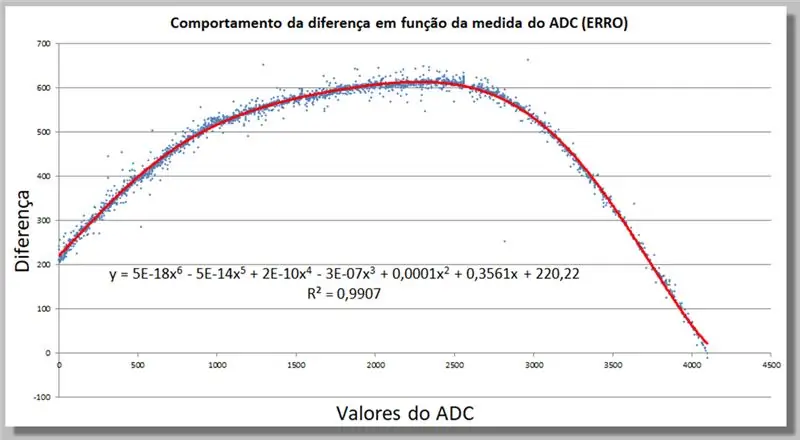
אנו יכולים לקבוע באקסל פונקציית תיקון על ידי הוספת קו מגמה, כיום ברמה גבוהה יותר, עד שיתאים מספיק לנתונים שלנו.

שלב 19: שימוש בתוכנות אחרות

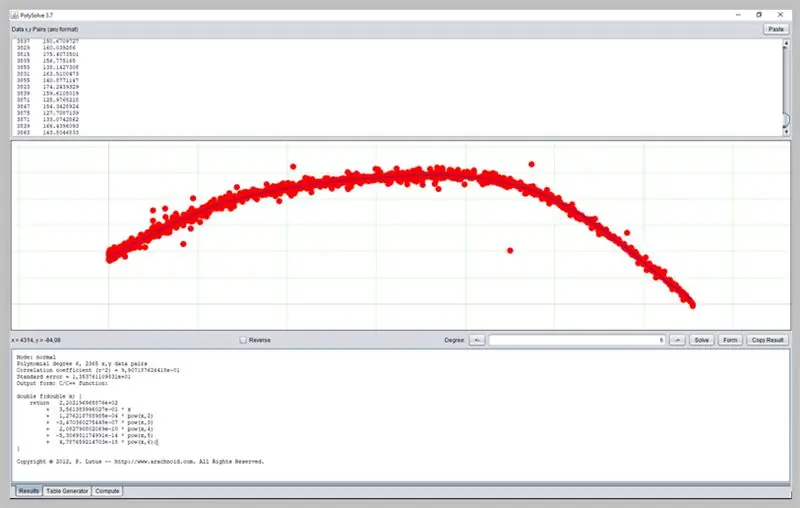
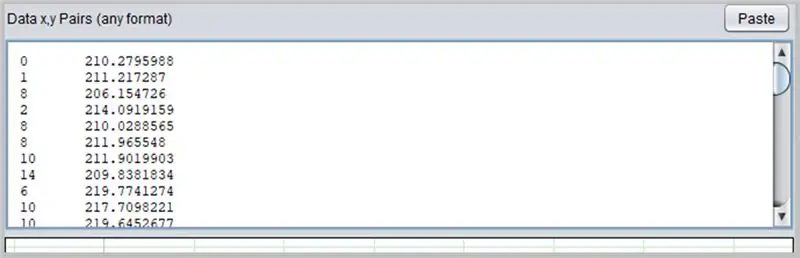
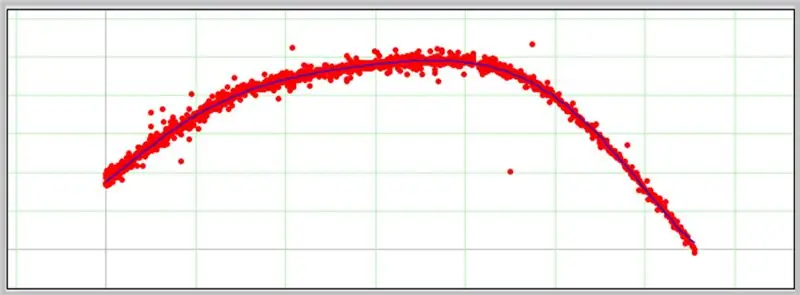
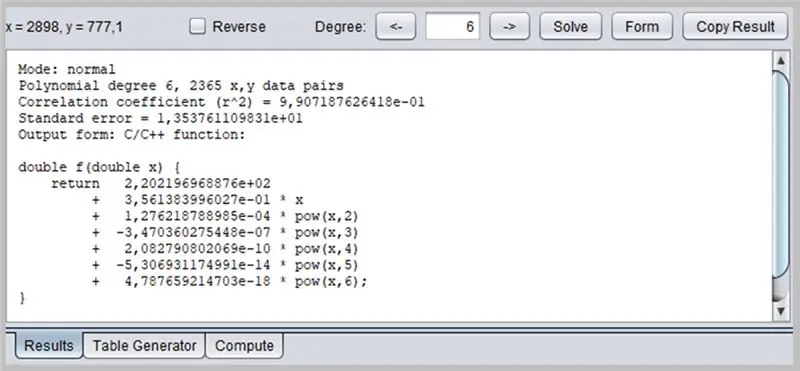
תוכנה מעניינת נוספת לקביעת עקומות היא PolySolve, שניתן להשתמש בה ישירות בקישור: https://arachnoid.com/polysolve/ או להורדה כיישום Java.

הוא מאפשר יישום של רגרסיות פולינומיות ברמה גבוהה יותר ומסירת הפונקציה המעוצבת, כמו גם פונקציות אחרות.

כדי להשתמש בו, פשוט הזן את הנתונים בתיבת הטקסט הראשונה. הנתונים חייבים לפעול לפי הסדר X, Y המופרד בפסיק או בכרטיסייה. נהג בזהירות בשימוש נכון בנקודה כנקודה עשרונית.

תרשים יופיע בתיבה הבאה אם הנתונים שהוזנו מעוצבים כראוי.

כך התפתחה עקומת השגיאות ADC שלנו.

חלון זה יציג את תוצאת הרגרסיה, כולל נתוני התאמת פונקציות, אשר בתורם יכולים להיות מעוצבים בפלט שלה בכמה אופנים: כפונקציה C / C ++, רשימת מקדמים, פונקציה שנכתבת ב- Java וכו '.

הערה: שימו לב למפרידי עשרוני

שלב 20: קבועים והתקנה ()

אני מציין כאן את ה- GPIO המשמש ללכידה אנלוגית. אני מאתחל את היציאה הסדרתית, כמו גם את הסיכה שנקבעה ללכידה אנלוגית.

const int pin_leitura = 36; // GPIO usado para captura analógica הגדרת חלל () {Serial.begin (1000000); // Iniciciando a porta somente sera para debug pinMode (pin_leitura, INPUT); // Pino utilizado para captura analógica}

שלב 21: לולאה () ופונקציית התיקון

אנו מבצעים את לכידת המתח המותאם, ומדפיסים את הערכים עם או בלי התיקונים הנכונים.

לולאת void () {int valor_analogico = analogRead (pin_leitura); // realiza a captura da tensão ajustada //Serial.print(valor_analogico + f (valor_analogico)); // imprime os valores para debug (COM CORREÇÃO) Serial.print (valor_analogico); // imprimime os valores para debug (SEM CORREÇÃO) Serial.print (","); Serial.print (4095); // cria uma linha para marcar o valor máximo de 4095 Serial.print (","); Serial.println (0); // cria uma linha para marcar o valor mínimo de 0}

שימו לב בשורה 12 שיש לנו אפשרות להדפיס את הנתונים בתוספת פונקציית ההבדל f (analog_value).

שלב 22: שימוש בפונקציית תיקון PolySolve

כאן אנו משתמשים בפונקציה PolySolve בתוך ה- Arduino IDE.

/* מצב: תואר פולינומי רגיל 6, 2365 x, y זוגות נתונים מקדם מתאם (r^2) = 9, 907187626418e-01 שגיאה רגילה = 1, 353761109831e+01 טופס פלט: פונקציית C/C ++: זכויות יוצרים © 2012, P. לוטוס - https://www.arachnoid.com. כל הזכויות שמורות. */ כפול f (כפול x) {החזרה 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e- 10 * pow (x, 4) + -5.306931174991e-14 * pow (x, 5) + 4.787659214703e-18 * pow (x, 6); }

שים לב לשינוי בפסיק נקודה כמפריד העשרוני.

שלב 23: לכידה באמצעות תיקון - סדרת פלוטר

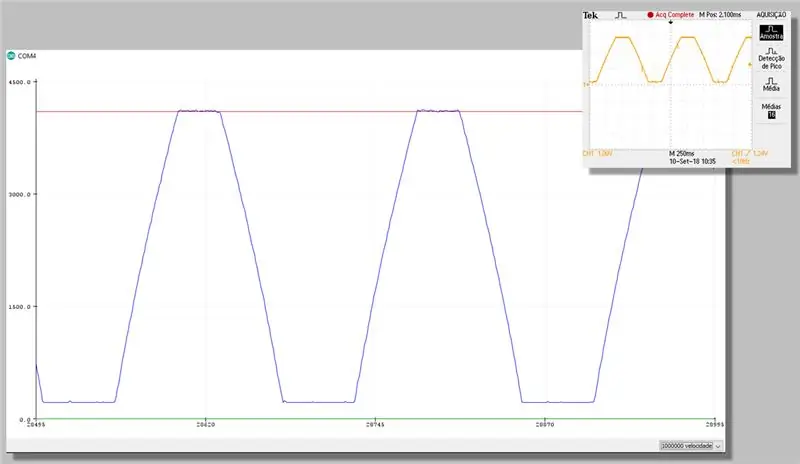
שלב 24: עלות חישובית

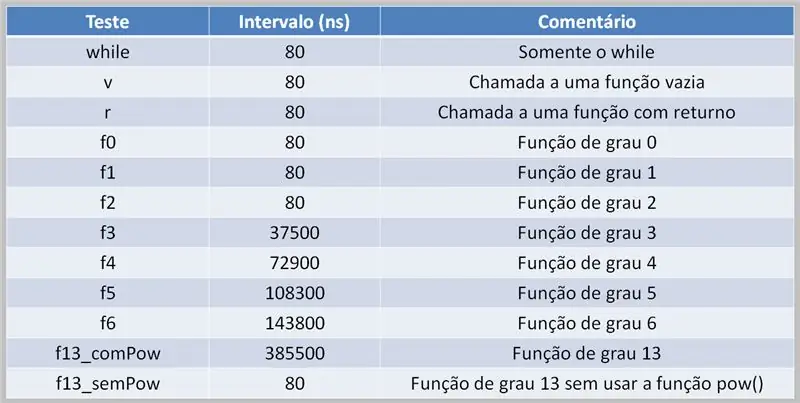
כדי לבצע חישובים פולינומיים, יש צורך שהמעבד יטפל במשימה זו. זה יכול להוביל לעיכובים בביצוע, בהתאם לקוד המקור וכוח המחשוב הזמין.

כאן, אנו רואים טבלת תוצאות של בדיקה באמצעות פולינומים מרובי תארים. שימו לב להבדל בין הזמנים שבהם נעשה שימוש בפונקציה pow () לבין כאשר לא.

שלב 25: קוד בדיקה - התקנה () והתחלת לולאה ()

הנה, יש לנו את הקוד המשמש בבדיקה שלנו.

הגדרת void () {Serial.begin (1000000); // Iniciando a porta serial somente para debug} לולאת חלל () {float valor_analogico = 500.0; // um valor arbtrario float quantidade = 10000.0; // quantidade de chamadas float contador = 0.0; // contador de chamadas

שלב 26: קוד בדיקה - לולאה () ועיבוד

השתמשתי בפונקציה micros () כדי לקבל את הערך במיקרו שניות.

// ============== inicia o processo float agora = micros (); // marca o instante inicial while (contador <quantidade) {// v (valor_analogico); // função vazia // r (valor_analogico); // função com retorno // f0 (valor_analogico); // grau 0 // f1 (valor_analogico); // grau 1 // f2 (valor_analogico); // grau 2 // f3 (valor_analogico); // grau 3 // f4 (valor_analogico); // grau 4 // f5 (valor_analogico); // grau 5 // f6 (valor_analogico); // grau 6 // f13_semPow (valor_analogico); // grau 13º SEM a função POW // f13_comPow (valor_analogico); // grau 13º COM a função שבויים ++; } agora = (micros () - agora) / quantidade; // determina o intervalo que se passou para cada iteração // ============= finaliza o processo

שלב 27: קוד בדיקה - לולאה () - תוצאות

אנו מדפיסים את הערך המוחזר מהפונקציה בדרגה 13 עם ובלי POW לצורך השוואה, כמו גם מרווח העיבוד.

// imprime o valor retornado da função de grau 13 com e sem POW para comparação Serial.print (f13_semPow (valor_analogico)); // grau 13º SEM a função שבויים Serial.print (" -"); Serial.print (f13_comPow (valor_analogico)); // grau 13º COM a função שבויים Serial.print (" -"); // imprime o intervalo do processamento Serial.println (אגורה, 6); }

שלב 28: קוד בדיקה - פונקציות משומשות

פונקציות ריקות (רק עם החזרה) של דרגה 0 ו -1.

// FUNÇÃO VAZI כפול v (כפול x) {} // FUNÇÃO SOMENTE COM RETORNO כפול r (כפול x) {החזר x; } // FUNÇÃO DE GRAU 0 כפול f0 (כפול x) {החזרה 2.202196968876e+02; } // FUNÇÃO DE GRAU 1 כפול f1 (כפול x) {החזרה 2.202196968876e + 02 + 3.561383996027e-01 * x; }

פונקציות בדרגה 2, 3 ו -4.

// FUNÇÃO DE GRAU 2 כפול f2 (כפול x) {החזרה 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2); } // FUNÇÃO DE GRAU 3 כפול f3 (כפול x) {החזרה 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3)); } // FUNÇÃO DE GRAU 4 כפול f4 (כפול x) {החזרה 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e-10 * pow (x, 4); }

פונקציות כיתה 5 ו -6.

// FUNÇÃO DE GRAU 5 כפול f5 (כפול x) {החזרה 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e-10 * pow (x, 4) + -5.306931174991e-14 * pow (x, 5); } // FUNÇÃO DE GRAU 6 כפול f6 (כפול x) {החזרה 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e-10 * pow (x, 4) + -5.306931174991e-14 * pow (x, 5) + 4.787659214703e-18 * pow (x, 6); }

פונקציה בדרגה 13 באמצעות השבויים.

// FUNÇÃO DE GRAU 13 USANDO O POW כפול f13_comPow (כפול x) {return 2, 161282383460e + 02 + 3, 944594843419e-01 * x + 5, 395439724295e-04 * pow (x, 2) + -3, 968558178426e-06 * pow (x, 3) + 1, 047910519933e-08 * pow (x, 4) + -1, 479271312313e-11 * pow (x, 5) + 1, 220894795714e-14 * pow (x, 6) + -6, 136200785076e-18 * pow (x, 7) + 1, 910015248179e-21 * pow (x, 8) + -3, 566607830903e-25 * pow (x, 9) + 5, 000280815521e-30 * pow (x, 10) + 3, 434515045670e-32 * pow (x, 11) + -1, 407635444704e-35 * pow (x, 12) + 9, 871816383223e-40 * pow (x, 13); }

פונקציה בדרגה 13 ללא שימוש ב- POW.

// FUNÇÃO DE GRAU SEM USAR O POW כפול f13_semPow (כפול x) {return 2, 161282383460e + 02 + 3, 944594843419e-01 * x + 5, 395439724295e-04 * x * x + -3, 968558178426e-06 * x * x * x + 1, 047910519933e-08 * x * x * x * x + -1, 479271312313e-11 * x * x * x * x * x + 1, 220894795714e-14 * x * x * x * x * x * x + -6, 136200785076e-18 * x * x * x * x * x * x * x + 1, 910015248179e-21 * x * x * x * x * x * x * x * x + -3, 566607830903e- 25 * x * x * x * x * x * x * x * x * x + 5, 000280815521e-30 * x * x * x * x * x * x * x * x * x * x + 3, 434515045670e- 32 * x * x * x * x * x * x * x * x * x * x * x + -1, 407635444704e -35 * x * x * x * x * x * x * x * x * x * x * x * x + 9, 871816383223e-40 * x * x * x * x * x * x * x * x * x * x * x * x; }

שלב 29: קבצים

הורד את הקבצים:

PDF

INO

גיליון אלקטרוני